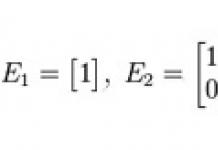தீர்மானியைப் பயன்படுத்தி தலைகீழ் அணியைக் கண்டறிதல். தலைகீழ் மேட்ரிக்ஸைக் கணக்கிடுவதற்கான அல்காரிதம். எலிமெண்டரி மேட்ரிக்ஸ் மாற்றங்கள்

n வது வரிசையின் சதுர அணி இருக்கட்டும்

மேட்ரிக்ஸ் ஏ -1 என்று அழைக்கப்படுகிறது தலைகீழ் அணிஅணி A தொடர்பாக, A*A -1 = E எனில், E என்பது nவது வரிசையின் அடையாள அணி.

முற்றொருமை- அத்தகைய ஒரு சதுர அணி, இதில் பிரதான மூலைவிட்டத்தில் உள்ள அனைத்து உறுப்புகளும், மேல் இடது மூலையில் இருந்து கீழ் வலது மூலையில் கடந்து செல்லும், ஒன்று, மீதமுள்ளவை பூஜ்ஜியங்கள், எடுத்துக்காட்டாக:

தலைகீழ் அணிஇருக்கலாம் சதுர மெட்ரிக்குகளுக்கு மட்டுமேஅந்த. வரிசைகள் மற்றும் நெடுவரிசைகளின் எண்ணிக்கை ஒத்துப்போகும் மெட்ரிக்குகளுக்கு.

தலைகீழ் மேட்ரிக்ஸின் இருப்பு நிலைக்கான தேற்றம்

ஒரு அணி தலைகீழ் அணியைப் பெறுவதற்கு, அது ஒருமை அல்லாததாக இருப்பது அவசியம் மற்றும் போதுமானது.

அணி A = (A1, A2,...A n) எனப்படும் சீரழியாத, நெடுவரிசை திசையன்கள் நேரியல் சார்பற்றதாக இருந்தால். மேட்ரிக்ஸின் நேரியல் சார்பற்ற நெடுவரிசை திசையன்களின் எண்ணிக்கை மேட்ரிக்ஸின் தரவரிசை என்று அழைக்கப்படுகிறது. எனவே, ஒரு தலைகீழ் அணி இருப்பதற்கு, மேட்ரிக்ஸின் தரவரிசை அதன் பரிமாணத்திற்கு சமமாக இருப்பது அவசியம் மற்றும் போதுமானது என்று நாம் கூறலாம், அதாவது. r = n.

தலைகீழ் மேட்ரிக்ஸைக் கண்டறிவதற்கான அல்காரிதம்

காஸியன் முறையைப் பயன்படுத்தி சமன்பாடுகளின் அமைப்புகளைத் தீர்ப்பதற்கான மேட்ரிக்ஸ் A ஐ அட்டவணையில் எழுதவும், அதற்கு வலதுபுறத்தில் மேட்ரிக்ஸ் E ஐ ஒதுக்கவும் (சமன்பாடுகளின் வலது பக்கங்களுக்குப் பதிலாக).
ஜோர்டான் மாற்றங்களைப் பயன்படுத்தி, அணி A ஐ அலகு நெடுவரிசைகளைக் கொண்ட அணியாகக் குறைக்கவும்; இந்த வழக்கில், மேட்ரிக்ஸ் E ஐ ஒரே நேரத்தில் மாற்றுவது அவசியம்.
தேவைப்பட்டால், கடைசி அட்டவணையின் வரிசைகளை (சமன்பாடுகள்) மறுசீரமைக்கவும், இதன் மூலம் அசல் அட்டவணையின் அணி A இன் கீழ் நீங்கள் அடையாள அணி E ஐப் பெறுவீர்கள்.
அசல் அட்டவணையின் மேட்ரிக்ஸ் E இன் கீழ் கடைசி அட்டவணையில் அமைந்துள்ள தலைகீழ் அணி A -1 ஐ எழுதவும்.

எடுத்துக்காட்டு 1

அணி Aக்கு, தலைகீழ் அணி A -1 ஐக் கண்டறியவும்

தீர்வு: மேட்ரிக்ஸ் A ஐ எழுதி, அடையாள அணி E ஐ வலதுபுறமாக ஒதுக்குகிறோம். ஜோர்டான் மாற்றங்களைப் பயன்படுத்தி, அணி A ஐ அடையாள அணி E ஆகக் குறைக்கிறோம். கணக்கீடுகள் அட்டவணை 31.1 இல் கொடுக்கப்பட்டுள்ளன.

அசல் அணி A மற்றும் தலைகீழ் அணி A -1 ஐப் பெருக்கி கணக்கீடுகளின் சரியான தன்மையை சரிபார்க்கலாம்.

மேட்ரிக்ஸ் பெருக்கத்தின் விளைவாக, அடையாள அணி பெறப்பட்டது. எனவே, கணக்கீடுகள் சரியாக செய்யப்பட்டன.

பதில்:

மேட்ரிக்ஸ் சமன்பாடுகளைத் தீர்ப்பது

மேட்ரிக்ஸ் சமன்பாடுகள் இப்படி இருக்கலாம்:

AX = B, HA = B, AXB = C,

இதில் A, B, C ஆகியவை குறிப்பிடப்பட்ட அணிகள், X என்பது விரும்பிய அணி.

மேட்ரிக்ஸ் சமன்பாடுகள் சமன்பாட்டை தலைகீழ் மெட்ரிக்குகளால் பெருக்குவதன் மூலம் தீர்க்கப்படுகின்றன.

எடுத்துக்காட்டாக, சமன்பாட்டிலிருந்து மேட்ரிக்ஸைக் கண்டுபிடிக்க, நீங்கள் இந்த சமன்பாட்டை இடதுபுறத்தில் பெருக்க வேண்டும்.

எனவே, சமன்பாட்டிற்கு ஒரு தீர்வைக் கண்டுபிடிக்க, நீங்கள் தலைகீழ் அணியைக் கண்டுபிடித்து சமன்பாட்டின் வலது பக்கத்தில் உள்ள மேட்ரிக்ஸால் பெருக்க வேண்டும்.

மற்ற சமன்பாடுகளும் இதேபோல் தீர்க்கப்படுகின்றன.

எடுத்துக்காட்டு 2

AX = B என்றால் சமன்பாட்டை தீர்க்கவும்

தீர்வு: தலைகீழ் அணி சமமாக இருப்பதால் (எடுத்துக்காட்டு 1 ஐப் பார்க்கவும்)

பொருளாதார பகுப்பாய்வில் மேட்ரிக்ஸ் முறை

மற்றவர்களுடன், அவைகளும் பயன்படுத்தப்படுகின்றன அணி முறைகள். இந்த முறைகள் நேரியல் மற்றும் வெக்டர்-மேட்ரிக்ஸ் இயற்கணிதத்தை அடிப்படையாகக் கொண்டவை. இத்தகைய முறைகள் சிக்கலான மற்றும் பல பரிமாண பொருளாதார நிகழ்வுகளை பகுப்பாய்வு செய்ய பயன்படுத்தப்படுகின்றன. பெரும்பாலும், இந்த முறைகள் நிறுவனங்களின் செயல்பாடு மற்றும் அவற்றின் கட்டமைப்பு பிரிவுகளின் ஒப்பீட்டு மதிப்பீட்டைச் செய்ய வேண்டியிருக்கும் போது பயன்படுத்தப்படுகின்றன.

மேட்ரிக்ஸ் பகுப்பாய்வு முறைகளைப் பயன்படுத்தும் செயல்பாட்டில், பல நிலைகளை வேறுபடுத்தி அறியலாம்.

முதல் கட்டத்தில்பொருளாதார குறிகாட்டிகளின் அமைப்பு உருவாக்கப்படுகிறது மற்றும் அதன் அடிப்படையில் ஆரம்ப தரவுகளின் அணி தொகுக்கப்படுகிறது, இது ஒரு அட்டவணையில் கணினி எண்கள் அதன் தனிப்பட்ட வரிசைகளில் காட்டப்படுகின்றன. (i = 1,2,....,n), மற்றும் செங்குத்து நெடுவரிசைகளில் - குறிகாட்டிகளின் எண்கள் (j = 1,2,....,m).

இரண்டாவது கட்டத்தில்ஒவ்வொரு செங்குத்து நெடுவரிசைக்கும், கிடைக்கக்கூடிய காட்டி மதிப்புகளில் மிகப்பெரியது அடையாளம் காணப்பட்டுள்ளது, இது ஒன்றாக எடுத்துக் கொள்ளப்படுகிறது.

இதற்குப் பிறகு, இந்த நெடுவரிசையில் பிரதிபலிக்கும் அனைத்து அளவுகளும் மிகப்பெரிய மதிப்பால் வகுக்கப்படுகின்றன மற்றும் தரப்படுத்தப்பட்ட குணகங்களின் அணி உருவாகிறது.

மூன்றாவது கட்டத்தில்மேட்ரிக்ஸின் அனைத்து கூறுகளும் சதுரமாக உள்ளன. அவை வெவ்வேறு முக்கியத்துவத்தைக் கொண்டிருந்தால், ஒவ்வொரு மேட்ரிக்ஸ் காட்டிக்கும் ஒரு குறிப்பிட்ட எடை குணகம் ஒதுக்கப்படும் கே. பிந்தைய மதிப்பு நிபுணர் கருத்து மூலம் தீர்மானிக்கப்படுகிறது.

கடைசியில், நான்காவது நிலைமதிப்பீடு மதிப்புகளைக் கண்டறிந்தது ஆர் ஜேஅவற்றின் அதிகரிப்பு அல்லது குறைப்பு வரிசையில் தொகுக்கப்படுகின்றன.

கோடிட்டுக் காட்டப்பட்ட மேட்ரிக்ஸ் முறைகள் பயன்படுத்தப்பட வேண்டும், எடுத்துக்காட்டாக, பல்வேறு முதலீட்டு திட்டங்களின் ஒப்பீட்டு பகுப்பாய்விலும், நிறுவனங்களின் செயல்பாடுகளின் பிற பொருளாதார குறிகாட்டிகளை மதிப்பிடுவதிலும்.

எந்த ஒருமை அல்லாத அணி A-க்கும் ஒரு தனி அணி A -1 உள்ளது

A*A -1 =A -1 *A = E,

இதில் E என்பது A போன்ற அதே வரிசைகளின் அடையாள அணியாகும். A -1 அணி A இன் தலைகீழ் என அழைக்கப்படுகிறது.

யாராவது மறந்துவிட்டால், அடையாள அணியில், மூலைவிட்டம் நிரப்பப்பட்டதைத் தவிர, மற்ற எல்லா நிலைகளும் பூஜ்ஜியங்களால் நிரப்பப்படும், அடையாள அணிக்கு எடுத்துக்காட்டு:

அட்ஜோயிண்ட் மேட்ரிக்ஸ் முறையைப் பயன்படுத்தி தலைகீழ் அணியைக் கண்டறிதல்

தலைகீழ் அணி சூத்திரத்தால் வரையறுக்கப்படுகிறது:

எங்கே A ij - உறுப்புகள் a ij.

அந்த. தலைகீழ் மேட்ரிக்ஸைக் கணக்கிட, இந்த மேட்ரிக்ஸின் தீர்மானிப்பதை நீங்கள் கணக்கிட வேண்டும். பின்னர் அதன் அனைத்து உறுப்புகளுக்கும் இயற்கணித நிரப்பிகளைக் கண்டறிந்து அவற்றிலிருந்து ஒரு புதிய அணியை உருவாக்கவும். அடுத்து இந்த மேட்ரிக்ஸை நீங்கள் கொண்டு செல்ல வேண்டும். புதிய மேட்ரிக்ஸின் ஒவ்வொரு உறுப்பையும் அசல் மேட்ரிக்ஸின் தீர்மானிப்பாளரால் வகுக்கவும்.

ஒரு சில உதாரணங்களைப் பார்ப்போம்.

ஒரு அணிக்கு A -1 ஐக் கண்டறியவும்

தீர்வு.அட்ஜோயிண்ட் மேட்ரிக்ஸ் முறையைப் பயன்படுத்தி A -1 ஐக் கண்டுபிடிப்போம். எங்களிடம் det A = 2 உள்ளது. அணி A இன் தனிமங்களின் இயற்கணித நிரப்புகளைக் கண்டுபிடிப்போம். இந்த விஷயத்தில், மேட்ரிக்ஸ் உறுப்புகளின் இயற்கணித நிரப்புகள், சூத்திரத்தின்படி ஒரு அடையாளத்துடன் எடுக்கப்பட்ட மேட்ரிக்ஸின் தொடர்புடைய கூறுகளாக இருக்கும்.

எங்களிடம் A 11 = 3, A 12 = -4, A 21 = -1, A 22 = 2. நாங்கள் இணை அணியை உருவாக்குகிறோம்

நாங்கள் அணி A* ஐக் கொண்டு செல்கிறோம்:

சூத்திரத்தைப் பயன்படுத்தி தலைகீழ் மேட்ரிக்ஸைக் காண்கிறோம்:

நாங்கள் பெறுகிறோம்:

அட்ஜோயிண்ட் மேட்ரிக்ஸ் முறையைப் பயன்படுத்தி, A -1 ஐக் கண்டறியவும்

தீர்வு. முதலில், தலைகீழ் மேட்ரிக்ஸின் இருப்பை சரிபார்க்க இந்த மேட்ரிக்ஸின் வரையறையை கணக்கிடுகிறோம். எங்களிடம் உள்ளது

இங்கே நாம் இரண்டாவது வரிசையின் உறுப்புகளில் மூன்றாவது வரிசையின் கூறுகளைச் சேர்த்துள்ளோம், முன்பு (-1) பெருக்கப்பட்டது, பின்னர் இரண்டாவது வரிசைக்கான தீர்மானிப்பதை விரிவுபடுத்தினோம். இந்த மேட்ரிக்ஸின் வரையறை பூஜ்ஜியத்திலிருந்து வேறுபட்டது என்பதால், அதன் தலைகீழ் அணி உள்ளது. இணை அணியை உருவாக்க, இந்த மேட்ரிக்ஸின் தனிமங்களின் இயற்கணித நிரப்புகளைக் காண்கிறோம். எங்களிடம் உள்ளது

சூத்திரத்தின் படி

போக்குவரத்து அணி A*:

பின்னர் சூத்திரத்தின் படி

அடிப்படை மாற்றங்களின் முறையைப் பயன்படுத்தி தலைகீழ் மேட்ரிக்ஸைக் கண்டறிதல்

சூத்திரத்தில் இருந்து வரும் தலைகீழ் அணியைக் கண்டறியும் முறையுடன் (அடுத்த அணி முறை), தலைகீழ் அணியைக் கண்டுபிடிப்பதற்கான ஒரு முறை உள்ளது, இது அடிப்படை மாற்றங்களின் முறை என்று அழைக்கப்படுகிறது.

எலிமெண்டரி மேட்ரிக்ஸ் மாற்றங்கள்

பின்வரும் மாற்றங்கள் எலிமெண்டரி மேட்ரிக்ஸ் உருமாற்றங்கள் என்று அழைக்கப்படுகின்றன:

1) வரிசைகளின் மறுசீரமைப்பு (நெடுவரிசைகள்);

2) ஒரு வரிசையை (நெடுவரிசையை) பூஜ்ஜியத்தைத் தவிர வேறு எண்ணால் பெருக்குதல்;

3) ஒரு வரிசையின் உறுப்புகளுடன் (நெடுவரிசை) மற்றொரு வரிசையின் (நெடுவரிசை) தொடர்புடைய கூறுகளைச் சேர்ப்பது, முன்பு ஒரு குறிப்பிட்ட எண்ணால் பெருக்கப்பட்டது.

அணி A -1 ஐக் கண்டறிய, ஒரு செவ்வக அணி B = (A|E) ஆர்டர்களை (n; 2n) உருவாக்குகிறோம், வலதுபுறத்தில் உள்ள அணி A க்கு ஒரு பிரிக்கும் கோட்டின் மூலம் அடையாள அணி E ஐ ஒதுக்குகிறோம்:

ஒரு உதாரணத்தைப் பார்ப்போம்.

அடிப்படை மாற்றங்களின் முறையைப் பயன்படுத்தி, A -1 ஐக் கண்டறியவும்

தீர்வு. நாங்கள் மேட்ரிக்ஸ் B ஐ உருவாக்குகிறோம்:

அணி B இன் வரிசைகளை α 1, α 2, α 3 ஆல் குறிப்போம். மேட்ரிக்ஸ் B இன் வரிசைகளில் பின்வரும் மாற்றங்களைச் செய்வோம்.

இந்த தலைப்பு மாணவர்களிடையே மிகவும் வெறுக்கப்படும் ஒன்றாகும். மோசமான, அநேகமாக, தகுதிகள் உள்ளன.

தந்திரம் என்னவென்றால், ஒரு தலைகீழ் தனிமத்தின் கருத்து (மற்றும் நான் மெட்ரிக்குகளைப் பற்றி மட்டும் பேசவில்லை) பெருக்கத்தின் செயல்பாட்டைக் குறிக்கிறது. பள்ளி பாடத்திட்டத்தில் கூட, பெருக்கல் ஒரு சிக்கலான செயல்பாடாகக் கருதப்படுகிறது, மேலும் மெட்ரிக்குகளின் பெருக்கல் பொதுவாக ஒரு தனித் தலைப்பாகும், இதற்காக நான் முழு பத்தியும் வீடியோ பாடமும் அர்ப்பணித்துள்ளேன்.

இன்று நாம் மேட்ரிக்ஸ் கணக்கீடுகளின் விவரங்களுக்கு செல்ல மாட்டோம். நினைவில் கொள்வோம்: மெட்ரிக்குகள் எவ்வாறு நியமிக்கப்படுகின்றன, அவை எவ்வாறு பெருக்கப்படுகின்றன, இதிலிருந்து பின்வருபவை என்ன.

விமர்சனம்: மேட்ரிக்ஸ் பெருக்கல்

முதலில், குறியீட்டை ஒப்புக்கொள்வோம். $\left[ m\times n \right]$ அளவுள்ள $A$ ஒரு அணியானது, சரியாக $m$ வரிசைகள் மற்றும் $n$ நெடுவரிசைகளைக் கொண்ட எண்களின் அட்டவணையாகும்:

\=\அண்டர்பிரேஸ்(\left[ \begin(matrix) ((a)_(11)) & ((a)_(12)) & ... & ((a)_(1n)) \\ (( a)_(21)) & ((a)_(22)) & ... & ((a)_(2n)) \\ ... & ... & ... & ... \\ ((a)_(m1)) & ((a)_(m2)) & ... & ((a)_(mn)) \\\ end(matrix) \right])_(n)\]

தற்செயலாக வரிசைகள் மற்றும் நெடுவரிசைகளைக் கலப்பதைத் தவிர்க்க (என்னை நம்புங்கள், தேர்வில் நீங்கள் ஒன்றை இரண்டுடன் குழப்பலாம், சில வரிசைகள் ஒருபுறம் இருக்க), படத்தைப் பாருங்கள்:

மேட்ரிக்ஸ் கலங்களுக்கான குறியீடுகளைத் தீர்மானித்தல்

என்ன நடக்கிறது? நீங்கள் நிலையான ஒருங்கிணைப்பு அமைப்பை $OXY$ மேல் இடது மூலையில் வைத்து, அச்சுகள் முழு அணியையும் உள்ளடக்கும் வகையில் இயக்கினால், இந்த மேட்ரிக்ஸின் ஒவ்வொரு கலமும் $\left(x;y \right)$ ஆயத்தொலைவுகளுடன் தனிப்பட்ட முறையில் இணைக்கப்படும். - இது வரிசை எண் மற்றும் நெடுவரிசை எண்ணாக இருக்கும்.

ஒருங்கிணைப்பு அமைப்பு ஏன் மேல் இடது மூலையில் வைக்கப்பட்டுள்ளது? ஆம், ஏனென்றால் அங்கிருந்துதான் நாம் எந்த நூல்களையும் படிக்கத் தொடங்குகிறோம். நினைவில் கொள்வது மிகவும் எளிது.

$x$ அச்சு ஏன் வலதுபுறமாக இல்லாமல் கீழ்நோக்கி இயக்கப்படுகிறது? மீண்டும், இது எளிமையானது: ஒரு நிலையான ஒருங்கிணைப்பு அமைப்பை எடுத்து ($x$ அச்சு வலதுபுறம் செல்கிறது, $y$ அச்சு மேலே செல்கிறது) அதை சுழற்று, அது மேட்ரிக்ஸை உள்ளடக்கும். இது 90 டிகிரி கடிகார திசையில் சுழற்சி - படத்தில் முடிவைப் பார்க்கிறோம்.

பொதுவாக, மேட்ரிக்ஸ் உறுப்புகளின் குறியீடுகளை எவ்வாறு தீர்மானிப்பது என்பதை நாங்கள் கண்டுபிடித்துள்ளோம். இப்போது பெருக்கத்தைப் பார்ப்போம்.

வரையறை. மெட்ரிக்குகள் $A=\left[ m\times n \right]$ மற்றும் $B=\left[ n\times k \right]$, முதலில் உள்ள நெடுவரிசைகளின் எண்ணிக்கை இரண்டாவது வரிசைகளின் எண்ணிக்கையுடன் ஒத்துப்போகும் போது, சீரானதாக அழைக்கப்படுகிறது.

சரியாக அந்த வரிசையில். ஒருவர் குழப்பமடைந்து $A$ மற்றும் $B$ ஆகிய மெட்ரிக்குகள் $\left(A;B \right)$ ஒரு ஆர்டர் ஜோடியை உருவாக்குகிறது என்று கூறலாம்: இந்த வரிசையில் அவை சீராக இருந்தால், $B என்று அவசியமில்லை. $ மற்றும் $A$ அவை. $\left(B;A \right)$ என்ற ஜோடியும் சீரானது.

பொருந்திய மெட்ரிக்குகளை மட்டுமே பெருக்க முடியும்.

வரையறை. $A=\left[ m\times n \right]$ மற்றும் $B=\left[ n\times k \right]$ ஆனது பொருந்திய மெட்ரிக்ஸின் தயாரிப்பு $C=\left[ m\times k \right ]$ , சூத்திரத்தின்படி $((c)_(ij))$ கணக்கிடப்படும் கூறுகள்:

\[((c)_(ij))=\sum\limits_(k=1)^(n)(((a)_(ik)))\cdot ((b)_(kj))\]

வேறு வார்த்தைகளில் கூறுவதானால்: $C=A\cdot B$ என்ற அணியின் $((c)_(ij))$ உறுப்பைப் பெற, நீங்கள் $j$ என்ற முதல் அணியின் $i$-வரிசையை எடுக்க வேண்டும். இரண்டாவது மேட்ரிக்ஸின் -வது நெடுவரிசை, பின்னர் இந்த வரிசை மற்றும் நெடுவரிசையிலிருந்து ஜோடி கூறுகளில் பெருக்கவும். முடிவுகளைச் சேர்க்கவும்.

ஆம், இது ஒரு கடுமையான வரையறை. அதிலிருந்து பல உண்மைகள் உடனடியாகப் பின்பற்றப்படுகின்றன:

மேட்ரிக்ஸ் பெருக்கல், பொதுவாகப் பேசுவது, பரிமாற்றம் அல்லாதது: $A\cdot B\ne B\cdot A$;
இருப்பினும், பெருக்கல் துணையாக உள்ளது: $\left(A\cdot B \right)\cdot C=A\cdot \left(B\cdot C \right)$;
மற்றும் விநியோகமாக: $\left(A+B \right)\cdot C=A\cdot C+B\cdot C$;
மீண்டும் ஒருமுறை விநியோகிக்கப்படுகிறது: $A\cdot \left(B+C \right)=A\cdot B+A\cdot C$.

பெருக்கல் செயல்பாட்டின் பரிமாற்றம் இல்லாததால் துல்லியமாக இடது மற்றும் வலது கூட்டுத் தொகைக் காரணிகளுக்குப் பெருக்கத்தின் பரவலானது தனித்தனியாக விவரிக்கப்பட வேண்டியிருந்தது.

$A\cdot B=B\cdot A$ என்று மாறினால், அத்தகைய மெட்ரிக்குகள் பரிமாற்றம் எனப்படும்.

அங்கு ஏதோவொன்றால் பெருக்கப்படும் அனைத்து மெட்ரிக்குகளிலும், சிறப்புகள் உள்ளன - அவை, எந்த மேட்ரிக்ஸால் $A$ பெருக்கப்படும்போது, மீண்டும் $A$ கொடுக்கின்றன:

வரையறை. $A\cdot E=A$ அல்லது $E\cdot A=A$ எனில் $E$ அணி அடையாளம் எனப்படும். சதுர அணி $A$ விஷயத்தில் நாம் எழுதலாம்:

மேட்ரிக்ஸ் சமன்பாடுகளைத் தீர்க்கும்போது அடையாள அணி அடிக்கடி விருந்தினராக இருக்கும். பொதுவாக, மெட்ரிக்ஸ் உலகில் அடிக்கடி விருந்தினர். :)

மேலும் இதன் காரணமாக $E$, அடுத்து எழுதப்படும் அனைத்து முட்டாள்தனங்களையும் யாரோ கொண்டு வந்தனர்.

தலைகீழ் அணி என்றால் என்ன

மேட்ரிக்ஸ் பெருக்கல் மிகவும் உழைப்பு மிகுந்த செயலாக இருப்பதால் (நீங்கள் பல வரிசைகள் மற்றும் நெடுவரிசைகளை பெருக்க வேண்டும்), தலைகீழ் மேட்ரிக்ஸின் கருத்தும் மிகவும் அற்பமானது அல்ல. மற்றும் சில விளக்கம் தேவை.

முக்கிய வரையறை

சரி, உண்மையை அறிய வேண்டிய நேரம் இது.

வரையறை. ஒரு அணி $B$ என்றால் ஒரு அணி $A$ இன் தலைகீழ் எனப்படும்

தலைகீழ் அணி $((A)^(-1))$ ஆல் குறிக்கப்படுகிறது (பட்டத்துடன் குழப்பமடையக்கூடாது!), எனவே வரையறையை பின்வருமாறு மீண்டும் எழுதலாம்:

எல்லாம் மிகவும் எளிமையானது மற்றும் தெளிவானது என்று தோன்றுகிறது. ஆனால் இந்த வரையறையை பகுப்பாய்வு செய்யும் போது, பல கேள்விகள் உடனடியாக எழுகின்றன:

தலைகீழ் அணி எப்போதும் உள்ளதா? எப்போதும் இல்லையென்றால், அதை எவ்வாறு தீர்மானிப்பது: அது எப்போது இருக்கிறது, எப்போது இல்லை?
அத்தகைய அணி ஒன்று இருப்பதாக யார் சொன்னார்கள்? சில ஆரம்ப அணி $A$ இல் தலைகீழ் கூட்டம் இருந்தால் என்ன செய்வது?
இந்த "தலைகீழ்" அனைத்தும் எப்படி இருக்கும்? எப்படி, சரியாக, நாம் அவற்றை எண்ண வேண்டும்?

கணக்கீட்டு வழிமுறைகளைப் பொறுத்தவரை, இதைப் பற்றி சிறிது நேரம் கழித்து பேசுவோம். ஆனால் மீதமுள்ள கேள்விகளுக்கு இப்போது பதிலளிப்போம். தனி அறிக்கைகள்-லெம்மாக்கள் வடிவில் அவற்றை உருவாக்குவோம்.

அடிப்படை பண்புகள்

$((A)^(-1))$ க்கு $A$, கொள்கையளவில், மேட்ரிக்ஸ் எப்படி இருக்க வேண்டும் என்பதில் இருந்து ஆரம்பிக்கலாம். இப்போது இந்த இரண்டு மெட்ரிக்குகளும் சதுரமாகவும், அதே அளவிலும் இருக்க வேண்டும் என்பதை உறுதி செய்வோம்: $\left[ n\times n \right]$.

லெம்மா 1. ஒரு அணி $A$ மற்றும் அதன் தலைகீழ் $((A)^(-1))$ கொடுக்கப்பட்டது. இந்த இரண்டு மெட்ரிக்குகளும் சதுரமாகவும், அதே வரிசையில் $n$ ஆகவும் இருக்கும்.

ஆதாரம். இது எளிமை. அணி $A=\left[ m\times n \right]$, $(A)^(-1))=\left[ a\times b \right]$. $A\cdot ((A)^(-1))=E$ என்பது வரையறையின்படி இருப்பதால், $A$ மற்றும் $(A)^(-1))$ மெட்ரிக்குகள் காட்டப்பட்டுள்ள வரிசையில் சீரானவை:

\[\begin(align) & \left[ m\times n \right]\cdot \left[ a\times b \right]=\left[ m\times b \right] \\ & n=a \end( சீரமை)\]

இது மேட்ரிக்ஸ் பெருக்கல் அல்காரிதத்தின் நேரடி விளைவு: $n$ மற்றும் $a$ குணகங்கள் "போக்குவரத்து" மற்றும் சமமாக இருக்க வேண்டும்.

அதே நேரத்தில், தலைகீழ் பெருக்கல் வரையறுக்கப்படுகிறது: $((A)^(-1))\cdot A=E$, எனவே மெட்ரிக்குகள் $((A)^(-1))$ மற்றும் $A$ மேலும் குறிப்பிட்ட வரிசையில் சீரானது:

\[\begin(align) & \left[ a\times b \right]\cdot \left[ m\times n \right]=\left[ a\times n \right] \\ & b=m \end( சீரமை)\]

எனவே, பொதுத்தன்மையை இழக்காமல், $A=\left[ m\times n \right]$, $((A)^(-1))=\left[ n\times m \right]$ என்று வைத்துக் கொள்ளலாம். இருப்பினும், $A\cdot ((A)^(-1))=(A)^(-1))\cdot A$ இன் வரையறையின்படி, மெட்ரிக்குகளின் அளவுகள் கண்டிப்பாக ஒத்துப்போகின்றன:

\[\begin(align) & \left[ m\times n \right]=\left[ n\times m \right] \\ & m=n \end(align)\]

$A$, $(A)^(-1))$ மற்றும் $E$ ஆகிய மூன்று மெட்ரிக்குகளும் $\left[ n\times n \right]$ அளவுள்ள சதுர மெட்ரிக்குகள் என்று மாறிவிடும். லெம்மா நிரூபிக்கப்பட்டுள்ளது.

சரி, அது ஏற்கனவே நல்லது. சதுர மெட்ரிக்குகள் மட்டுமே தலைகீழாக இருப்பதைக் காண்கிறோம். இப்போது தலைகீழ் அணி எப்போதும் ஒரே மாதிரியாக இருப்பதை உறுதி செய்வோம்.

லெம்மா 2. ஒரு அணி $A$ மற்றும் அதன் தலைகீழ் $((A)^(-1))$ கொடுக்கப்பட்டது. பின்னர் இந்த தலைகீழ் அணி மட்டுமே உள்ளது.

ஆதாரம். முரண்பாட்டின் மூலம் செல்லலாம்: $A$ அணிக்கு குறைந்தபட்சம் இரண்டு தலைகீழ்கள் இருக்கட்டும் - $B$ மற்றும் $C$. பின்னர், வரையறையின்படி, பின்வரும் சமத்துவங்கள் உண்மை:

\[\begin(align) & A\cdot B=B\cdot A=E; \\ & A\cdot C=C\cdot A=E. \\ \முடிவு(சீரமை)\]

லெம்மா 1 இலிருந்து, $A$, $B$, $C$ மற்றும் $E$ ஆகிய நான்கு மெட்ரிக்குகளும் ஒரே வரிசையின் சதுரங்கள் என்று முடிவு செய்கிறோம்: $\left[ n\times n \right]$. எனவே, தயாரிப்பு வரையறுக்கப்படுகிறது:

மேட்ரிக்ஸ் பெருக்கல் தொடர்புடையது (ஆனால் பரிமாற்றம் அல்ல!), நாம் எழுதலாம்:

\[\begin(align) & B\cdot A\cdot C=\left(B\cdot A \right)\cdot C=E\cdot C=C; \\ & B\cdot A\cdot C=B\cdot \left(A\cdot C \right)=B\cdot E=B; \\ & B\cdot A\cdot C=C=B\Rightarrow B=C. \\ \முடிவு(சீரமை)\]

எங்களுக்கு ஒரே சாத்தியமான விருப்பம் கிடைத்தது: தலைகீழ் மேட்ரிக்ஸின் இரண்டு பிரதிகள் சமம். லெம்மா நிரூபிக்கப்பட்டுள்ளது.

மேலே உள்ள வாதங்கள், $b\ne 0$ என்ற அனைத்து உண்மையான எண்களுக்கும் தலைகீழ் தனிமத்தின் தனித்தன்மையை நிரூபிக்கும். மெட்ரிக்குகளின் பரிமாணத்தை கணக்கில் எடுத்துக்கொள்வது மட்டுமே குறிப்பிடத்தக்க கூடுதலாகும்.

இருப்பினும், ஒவ்வொரு சதுர மேட்ரிக்ஸும் தலைகீழாக இருக்கிறதா என்பது பற்றி எங்களுக்கு இன்னும் எதுவும் தெரியாது. இங்கே தீர்மானிப்பான் எங்கள் உதவிக்கு வருகிறது - இது அனைத்து சதுர மெட்ரிக்குகளுக்கும் ஒரு முக்கிய பண்பு.

லெம்மா 3. ஒரு அணி $A$ கொடுக்கப்பட்டது. அதன் தலைகீழ் அணி $((A)^(-1))$ இருந்தால், அசல் மேட்ரிக்ஸின் நிர்ணயம் பூஜ்ஜியமல்ல:

\[\இடது| A\வலது|\ne 0\]

ஆதாரம். $A$ மற்றும் $(A)^(-1))$ என்பது $\இடது[ n\times n \right]$ அளவுள்ள சதுர மெட்ரிக்குகள் என்பதை நாங்கள் ஏற்கனவே அறிவோம். எனவே, அவை ஒவ்வொன்றிற்கும் நாம் தீர்மானிப்பதைக் கணக்கிடலாம்: $\left| ஏ\வலது|$ மற்றும் $\இடது| ((A)^(-1)) \right|$. எவ்வாறாயினும், ஒரு தயாரிப்பின் நிர்ணயிப்பானது தீர்மானிப்பவர்களின் தயாரிப்புக்கு சமம்:

\[\இடது| A\cdot B \right|=\left| A \right|\cdot \left| B \right|\Rightarrow \left| A\cdot ((A)^(-1)) \right|=\left| A \right|\cdot \left| ((A)^(-1)) \right|\]

ஆனால் வரையறையின்படி, $A\cdot ((A)^(-1))=E$, மற்றும் $E$ இன் நிர்ணயம் எப்பொழுதும் 1க்கு சமமாக இருக்கும்.

\[\begin(align) & A\cdot ((A)^(-1))=E; \\ & \இடது| A\cdot ((A)^(-1)) \right|=\left| E\right|; \\ & \இடது| A \right|\cdot \left| ((A)^(-1)) \right|=1. \\ \முடிவு(சீரமை)\]

இந்த எண்கள் ஒவ்வொன்றும் பூஜ்ஜியமாக இருந்தால் மட்டுமே இரண்டு எண்களின் பலன் ஒன்றுக்கு சமமாக இருக்கும்:

\[\இடது| A \right|\ne 0;\quad \left| ((A)^(-1)) \right|\ne 0.\]

அதனால் $\left| என்று மாறிவிடும் A \right|\ne 0$. லெம்மா நிரூபிக்கப்பட்டுள்ளது.

உண்மையில், இந்த தேவை மிகவும் தர்க்கரீதியானது. இப்போது நாம் தலைகீழ் மேட்ரிக்ஸைக் கண்டறிவதற்கான வழிமுறையை பகுப்பாய்வு செய்வோம் - மேலும் பூஜ்ஜியத்தை தீர்மானிப்பதன் மூலம், கொள்கையளவில் தலைகீழ் அணி ஏன் இருக்க முடியாது என்பது முற்றிலும் தெளிவாகிவிடும்.

ஆனால் முதலில், ஒரு "துணை" வரையறையை உருவாக்குவோம்:

வரையறை. ஒரு ஒற்றை அணி என்பது $\left[ n\times n \right]$ அளவுள்ள சதுர அணி ஆகும், அதன் நிர்ணயம் பூஜ்ஜியமாகும்.

எனவே, ஒவ்வொரு தலைகீழான மேட்ரிக்ஸும் ஒருமையற்றது என்று நாம் கூறலாம்.

மேட்ரிக்ஸின் தலைகீழ் எவ்வாறு கண்டுபிடிப்பது

இப்போது நாம் தலைகீழ் மெட்ரிக்குகளைக் கண்டுபிடிப்பதற்கான உலகளாவிய வழிமுறையைக் கருத்தில் கொள்வோம். பொதுவாக, பொதுவாக ஏற்றுக்கொள்ளப்பட்ட இரண்டு வழிமுறைகள் உள்ளன, மேலும் இன்று இரண்டாவதாகக் கருதுவோம்.

$\left[ 2\times 2 \right]$ மற்றும் - ஓரளவு - $\left[ 3\time 3 \right]$ அளவு மெட்ரிக்குகளுக்கு இப்போது விவாதிக்கப்படும் ஒன்று மிகவும் பயனுள்ளதாக இருக்கும். ஆனால் $\left[ 4\times 4 \right]$ என்ற அளவிலிருந்து தொடங்கி அதைப் பயன்படுத்தாமல் இருப்பது நல்லது. ஏன் - இப்போது நீங்களே எல்லாவற்றையும் புரிந்துகொள்வீர்கள்.

இயற்கணித சேர்த்தல்

தயாராய் இரு. இப்போது வலி இருக்கும். இல்லை, கவலைப்பட வேண்டாம்: ஒரு பாவாடையில் ஒரு அழகான செவிலியர், சரிகை கொண்ட காலுறைகள் உங்களிடம் வந்து பிட்டத்தில் ஒரு ஊசி போடாது. எல்லாமே மிகவும் புத்திசாலித்தனமானது: இயற்கணித சேர்த்தல் மற்றும் அவரது மாட்சிமை "யூனியன் மேட்ரிக்ஸ்" ஆகியவை உங்களிடம் வருகின்றன.

முக்கிய விஷயத்துடன் ஆரம்பிக்கலாம். $A=\left[ n\times n \right]$ அளவில் ஒரு சதுர அணி இருக்கட்டும், அதன் உறுப்புகள் $((a)_(ij))$ என அழைக்கப்படுகின்றன. அத்தகைய ஒவ்வொரு உறுப்புக்கும் நாம் ஒரு இயற்கணித நிரப்பியை வரையறுக்கலாம்:

வரையறை. $A=\இடதுபுறத்தில் உள்ள $i$வது வரிசையிலும் $j$வது நெடுவரிசையிலும் அமைந்துள்ள $((a)_(ij))$ உறுப்பிற்கு இயற்கணித நிரப்பு $((A)_(ij))$ n \times n \right]$ என்பது படிவத்தின் கட்டுமானமாகும்

\[((A)_(ij))=((\left(-1 \right))^(i+j))\cdot M_(ij)^(*)\]

$M_(ij)^(*)$ என்பது அதே $i$வது வரிசையையும் $j$வது நெடுவரிசையையும் நீக்குவதன் மூலம் அசல் $A$ இலிருந்து பெறப்பட்ட மேட்ரிக்ஸின் நிர்ணயம் ஆகும்.

மீண்டும். $\left(i;j \right)$ ஆயத்தொலைவுகளுடன் கூடிய மேட்ரிக்ஸ் உறுப்புக்கான இயற்கணித நிரப்பு $(A)_(ij))$ என குறிக்கப்படுகிறது மற்றும் திட்டத்தின் படி கணக்கிடப்படுகிறது:

முதலில், அசல் மேட்ரிக்ஸிலிருந்து $i$-வரிசை மற்றும் $j$-வது நெடுவரிசையை நீக்குவோம். நாங்கள் ஒரு புதிய சதுர மேட்ரிக்ஸைப் பெறுகிறோம், அதன் தீர்மானத்தை $M_(ij)^(*)$ எனக் குறிப்பிடுகிறோம்.
இந்த தீர்மானத்தை நாம் $((\left(-1 \right))^(i+j))$ ஆல் பெருக்குகிறோம் - முதலில் இந்த வெளிப்பாடு மனதைக் கவரும் என்று தோன்றலாம், ஆனால் சாராம்சத்தில் நாம் முன்னால் உள்ள அடையாளத்தைக் கண்டுபிடிப்போம். $M_(ij)^(*) $.
நாங்கள் எண்ணி ஒரு குறிப்பிட்ட எண்ணைப் பெறுகிறோம். அந்த. இயற்கணிதக் கூட்டல் துல்லியமாக ஒரு எண், சில புதிய அணிகள் போன்றவை அல்ல.

அணி $M_(ij)^(*)$ தானே $((a)_(ij))$ உறுப்பின் கூடுதல் மைனர் என அழைக்கப்படுகிறது. இந்த அர்த்தத்தில், ஒரு இயற்கணித நிரப்புதலின் மேலே உள்ள வரையறை மிகவும் சிக்கலான வரையறையின் ஒரு சிறப்பு வழக்கு - தீர்மானிப்பதைப் பற்றிய பாடத்தில் நாம் பார்த்தது.

முக்கியமான குறிப்பு. உண்மையில், "வயது வந்தோர்" கணிதத்தில், இயற்கணிதக் கூட்டல்கள் பின்வருமாறு வரையறுக்கப்படுகின்றன:

சதுர அணியில் $k$ வரிசைகள் மற்றும் $k$ நெடுவரிசைகளை எடுக்கிறோம். அவற்றின் குறுக்குவெட்டில் $\left[ k\times k \right]$ அளவிலான மேட்ரிக்ஸைப் பெறுகிறோம் - அதன் நிர்ணயம் $k$ வரிசையின் மைனர் என்று அழைக்கப்படுகிறது மற்றும் $((M)_(k))$ எனக் குறிக்கப்படுகிறது.

இந்த "தேர்ந்தெடுக்கப்பட்ட" $k$ வரிசைகள் மற்றும் $k$ நெடுவரிசைகளை நாம் கடந்து செல்கிறோம். மீண்டும் ஒரு சதுர அணியைப் பெறுவீர்கள் - அதன் நிர்ணயம் கூடுதல் மைனர் என்று அழைக்கப்படுகிறது மற்றும் $M_(k)^(*)$ எனக் குறிக்கப்படுகிறது.

$M_(k)^(*)$ ஐ $(\இடது(-1 \வலது))^(t))$ ஆல் பெருக்கவும், இங்கு $t$ என்பது (இப்போது கவனம்!) தேர்ந்தெடுக்கப்பட்ட அனைத்து வரிசைகளின் எண்களின் கூட்டுத்தொகை மற்றும் நெடுவரிசைகள். இது இயற்கணிதக் கூட்டலாக இருக்கும்.

மூன்றாவது படியைப் பாருங்கள்: உண்மையில் $2k$ விதிமுறைகளின் தொகை உள்ளது! மற்றொரு விஷயம் என்னவென்றால், $k=1$ க்கு நாம் 2 விதிமுறைகளை மட்டுமே பெறுவோம் - இவை $i+j$ ஆக இருக்கும் - $((a)_(ij))$ என்ற உறுப்பின் "ஆயத்தொகுப்புகள்" ஒரு இயற்கணித நிரப்பியைத் தேடுகிறது.

எனவே இன்று நாம் சற்று எளிமைப்படுத்தப்பட்ட வரையறையைப் பயன்படுத்துகிறோம். ஆனால் நாம் பின்னர் பார்ப்போம், அது போதுமானதை விட அதிகமாக இருக்கும். பின்வரும் விஷயம் மிகவும் முக்கியமானது:

வரையறை. $A=\left[ n\times n \right]$ வரையிலான கூட்டு அணி $S$ என்பது $\left[ n\times n \right]$ அளவின் புதிய அணி ஆகும், இது $A$ இலிருந்து பெறப்பட்டது. $((a)_(ij))$ ஐ இயற்கணிதச் சேர்த்தல் மூலம் மாற்றுவதன் மூலம் $((A)_(ij))$:

\\Rightarrow S=\left[ \begin(matrix) ((A)_(11)) & ((A)_(12)) & ... & ((A)_(1n)) \\ ((( A)_(21)) & ((A)_(22)) & ... & (A)_(2n)) \\ ... & ... & ... & ... \\ ((A)_(n1)) & ((A)_(n2)) & ... & ((A)_(nn)) \\\ end(matrix) \right]\]

இந்த வரையறையை உணரும் தருணத்தில் எழும் முதல் எண்ணம் "எவ்வளவு கணக்கிடப்பட வேண்டும்!" நிதானமாக: நீங்கள் எண்ண வேண்டும், ஆனால் அவ்வளவு இல்லை. :)

சரி, இதெல்லாம் மிகவும் நன்றாக இருக்கிறது, ஆனால் அது ஏன் அவசியம்? ஆனால் ஏன்.

முக்கிய தேற்றம்

கொஞ்சம் பின்னோக்கிப் போவோம். நினைவில் கொள்ளுங்கள், லெம்மா 3 இல் தலைகீழான அணி $A$ எப்போதும் ஒருமை அல்ல என்று கூறப்பட்டது (அதாவது, அதன் நிர்ணயம் பூஜ்ஜியமல்ல: $\left| A \right|\ne 0$).

எனவே, இதற்கு நேர்மாறானது உண்மைதான்: $A$ அணி ஒருமையாக இல்லாவிட்டால், அது எப்போதும் தலைகீழாக இருக்கும். மேலும் $((A)^(-1))$க்கான தேடல் திட்டம் கூட உள்ளது. அதைப் பாருங்கள்:

தலைகீழ் அணி தேற்றம். ஒரு சதுர அணி $A=\left[ n\times n \right]$ கொடுக்கப்பட்டால், அதன் நிர்ணயம் பூஜ்ஜியமல்ல: $\left| A \right|\ne 0$. பின்னர் தலைகீழ் அணி $((A)^(-1))$ உள்ளது மற்றும் சூத்திரத்தால் கணக்கிடப்படுகிறது:

\[((A)^(-1))=\frac(1)(\left| A \right|)\cdot ((S)^(T))\]

இப்போது - எல்லாம் ஒன்றுதான், ஆனால் தெளிவான கையெழுத்தில். தலைகீழ் மேட்ரிக்ஸைக் கண்டுபிடிக்க, உங்களுக்கு இது தேவை:

தீர்மானிக்கும் $\left| A \right|$ மற்றும் அது பூஜ்ஜியம் அல்ல என்பதை உறுதிப்படுத்தவும்.
யூனியன் மேட்ரிக்ஸை $S$ உருவாக்கவும், அதாவது. 100500 இயற்கணிதக் கூட்டல்களை $((A)_(ij))$ எண்ணி $((a)_(ij))$ இடத்தில் வைக்கவும்.
இந்த மேட்ரிக்ஸை $S$ இடமாற்றி, பின்னர் $q=(1)/(\left| A \right|)\;$ என்ற எண்ணால் பெருக்கவும்.

அவ்வளவுதான்! தலைகீழ் அணி $((A)^(-1))$ கண்டறியப்பட்டது. எடுத்துக்காட்டுகளைப் பார்ப்போம்:

\[\left[ \begin(matrix) 3 & 1 \\ 5 & 2 \\\ end(matrix) \right]\]

தீர்வு. மீள்தன்மையை சரிபார்க்கலாம். தீர்மானிப்பதைக் கணக்கிடுவோம்:

\[\இடது| எ\வலது|=\இடது| \begin(matrix) 3 & 1 \\ 5 & 2 \\\ end(matrix) \right|=3\cdot 2-1\cdot 5=6-5=1\]

நிர்ணயம் பூஜ்ஜியத்திலிருந்து வேறுபட்டது. இதன் பொருள் மேட்ரிக்ஸ் தலைகீழானது. யூனியன் மேட்ரிக்ஸை உருவாக்குவோம்:

இயற்கணிதச் சேர்த்தல்களைக் கணக்கிடுவோம்:

\[\begin(align) & ((A)_(11))=((\left(-1 \right))^(1+1))\cdot \left| 2 \right|=2; \\ & ((A)_(12))=((\left(-1 \right))^(1+2))\cdot \left| 5 \right|=-5; \\ & ((A)_(21))=((\left(-1 \right))^(2+1))\cdot \left| 1 \right|=-1; \\ & ((A)_(22))=((\left(-1 \right))^(2+2))\cdot \left| 3\வலது|=3. \\ \முடிவு(சீரமை)\]

தயவுசெய்து கவனிக்கவும்: தீர்மானிப்பவர்கள் |2|, |5|, |1| மற்றும் |3| அளவு $\left[ 1\time 1 \right]$ அளவுகளை நிர்ணயிப்பவை, தொகுதிகள் அல்ல. அந்த. தீர்மானிப்பதில் எதிர்மறை எண்கள் இருந்தால், "கழித்தல்" அகற்ற வேண்டிய அவசியமில்லை.

மொத்தத்தில், எங்கள் யூனியன் மேட்ரிக்ஸ் இதுபோல் தெரிகிறது:

\[((A)^(-1))=\frac(1)(\left| A \right|)\cdot ((S)^(T))=\frac(1)(1)\cdot ( (\left[ \begin(array)(*(35)(r)) 2 & -5 \\ -1 & 3 \\\ end(array) \right])^(T))=\left[ \begin (வரிசை)(*(35)(r)) 2 & -1 \\ -5 & 3 \\\ end(array) \right]\]

சரி இப்போது எல்லாம் முடிந்துவிட்டது. பிரச்சனை தீர்ந்துவிட்டது.

பதில். $\left[ \begin(array)(*(35)(r)) 2 & -1 \\ -5 & 3 \\\ end(array) \right]$

பணி. தலைகீழ் மேட்ரிக்ஸைக் கண்டறியவும்:

\[\left[ \begin(array)(*(35)(r)) 1 & -1 & 2 \\ 0 & 2 & -1 \\ 1 & 0 & 1 \\\ end(array) \right] \]

தீர்வு. தீர்மானிப்பதை மீண்டும் கணக்கிடுகிறோம்:

\[\தொடங்கு(சீரமைக்க) & \இடது| \begin(array)(*(35)(r)) 1 & -1 & 2 \\ 0 & 2 & -1 \\ 1 & 0 & 1 \\\ end(array) \right|=\begin(matrix ) \left(1\cdot 2\cdot 1+\left(-1 \right)\cdot \left(-1 \right)\cdot 1+2\cdot 0\cdot 0 \right)- \\ -\left (2\cdot 2\cdot 1+\left(-1 \right)\cdot 0\cdot 1+1\cdot \left(-1 \right)\cdot 0 \right) \\\ end(matrix)= \ \ & =\left(2+1+0 \right)-\left(4+0+0 \right)=-1\ne 0. \\ \end(align)\]

தீர்மானிப்பான் பூஜ்ஜியமற்றது-மேட்ரிக்ஸ் தலைகீழானது. ஆனால் இப்போது அது மிகவும் கடினமாக இருக்கும்: நாம் 9 (ஒன்பது, மதர்ஃபக்கர்!) இயற்கணிதச் சேர்த்தல்களைக் கணக்கிட வேண்டும். மேலும் அவை ஒவ்வொன்றும் தீர்மானிக்கும் $\left[ 2\time 2 \right]$ ஐக் கொண்டிருக்கும். பறந்தது:

\[\begin(matrix) ((A)_(11))=((\left(-1 \right))^(1+1))\cdot \left| \begin(matrix) 2 & -1 \\ 0 & 1 \\\ end(matrix) \right|=2; \\ ((A)_(12))=((\left(-1 \right))^(1+2))\cdot \left| \begin(matrix) 0 & -1 \\ 1 & 1 \\\ end(matrix) \right|=-1; \\ ((A)_(13))=((\left(-1 \right))^(1+3))\cdot \left| \begin(matrix) 0 & 2 \\ 1 & 0 \\\ end(matrix) \right|=-2; \\ ... \\ ((A)_(33))=((\left(-1 \right))^(3+3))\cdot \left| \begin(matrix) 1 & -1 \\ 0 & 2 \\\ end(matrix) \right|=2; \\ \முடிவு(மேட்ரிக்ஸ்)\]

சுருக்கமாக, யூனியன் மேட்ரிக்ஸ் இப்படி இருக்கும்:

எனவே, தலைகீழ் அணி:

\[((A)^(-1))=\frac(1)(-1)\cdot \left[ \begin(matrix) 2 & -1 & -2 \\ 1 & -1 & -1 \\ -3 & 1 & 2 \\\ முடிவு(மேட்ரிக்ஸ்) \right]=\left[ \begin(array)(*(35)(r))-2 & -1 & 3 \\ 1 & 1 & -1 \ \2 & 1 & -2 \\\ முடிவு(வரிசை) \வலது]\]

அவ்வளவுதான். இதோ பதில்.

பதில். $\left[ \begin(array)(*(35)(r)) -2 & -1 & 3 \\ 1 & 1 & -1 \\ 2 & 1 & -2 \\\ end(array) \right ]$

நீங்கள் பார்க்க முடியும் என, ஒவ்வொரு உதாரணத்தின் முடிவிலும் நாங்கள் ஒரு காசோலை செய்தோம். இது சம்பந்தமாக, ஒரு முக்கிய குறிப்பு:

சரிபார்க்க சோம்பேறியாக இருக்க வேண்டாம். கிடைத்த தலைகீழ் அணி மூலம் அசல் அணியை பெருக்கவும் - நீங்கள் $E$ பெற வேண்டும்.

உதாரணமாக, நீங்கள் ஒரு மேட்ரிக்ஸ் சமன்பாட்டைத் தீர்க்கும்போது, மேலும் கணக்கீடுகளில் பிழையைத் தேடுவதை விட இந்தச் சரிபார்ப்பைச் செய்வது மிகவும் எளிதானது மற்றும் விரைவானது.

மாற்று வழி

நான் சொன்னது போல், தலைகீழ் அணி தேற்றம் $\left[ 2\times 2 \right]$ மற்றும் $\left[ 3\time 3 \right]$ அளவுகளுக்கு நன்றாக வேலை செய்கிறது ), ஆனால் பெரிய மெட்ரிக்குகளுக்கு சோகம் தொடங்குகிறது.

ஆனால் கவலைப்பட வேண்டாம்: $\left[ 10\times 10 \right]$ மேட்ரிக்ஸுக்கு கூட தலைகீழ் நிதானத்தைக் கண்டறியும் மாற்று வழிமுறை உள்ளது. ஆனால், அடிக்கடி நடப்பது போல, இந்த வழிமுறையைக் கருத்தில் கொள்ள நமக்கு ஒரு சிறிய தத்துவார்த்த பின்னணி தேவை.

அடிப்படை மாற்றங்கள்

சாத்தியமான அனைத்து மேட்ரிக்ஸ் மாற்றங்களிலும், பல சிறப்புகள் உள்ளன - அவை அடிப்படை என்று அழைக்கப்படுகின்றன. இதுபோன்ற மூன்று மாற்றங்கள் சரியாக உள்ளன:

பெருக்கல். நீங்கள் $i$வது வரிசையை (நெடுவரிசை) எடுத்து, $k\ne 0$ என்ற எண்ணால் பெருக்கலாம்;
கூட்டல். $k\ne 0$ என்ற எண்ணால் பெருக்கப்படும் $i$-வது வரிசையில் (நெடுவரிசை) வேறு ஏதேனும் $j$-வது வரிசையை (நெடுவரிசை) சேர்க்கவும் (நிச்சயமாக நீங்கள் $k=0$ செய்யலாம், ஆனால் என்ன புள்ளி? ? எதுவும் மாறாது).
மறுசீரமைப்பு. $i$th மற்றும் $j$th வரிசைகளை (நெடுவரிசைகள்) எடுத்து இடங்களை மாற்றவும்.

இந்த மாற்றங்கள் ஏன் ஆரம்பநிலை என்று அழைக்கப்படுகின்றன (பெரிய மெட்ரிக்குகளுக்கு அவை அவ்வளவு அடிப்படையாகத் தெரியவில்லை) ஏன் அவற்றில் மூன்று மட்டுமே உள்ளன - இந்தக் கேள்விகள் இன்றைய பாடத்தின் எல்லைக்கு அப்பாற்பட்டவை. எனவே, நாங்கள் விவரங்களுக்கு செல்ல மாட்டோம்.

மற்றொரு விஷயம் முக்கியமானது: இந்த அனைத்து வக்கிரங்களையும் நாம் அட்ஜோயிண்ட் மேட்ரிக்ஸில் செய்ய வேண்டும். ஆம், ஆம்: நீங்கள் கேட்டது சரிதான். இப்போது இன்னும் ஒரு வரையறை இருக்கும் - இன்றைய பாடத்தில் கடைசி.

இணை அணி

நிச்சயமாக பள்ளியில் நீங்கள் கூட்டல் முறையைப் பயன்படுத்தி சமன்பாடுகளின் அமைப்புகளைத் தீர்த்தீர்கள். சரி, அங்கே, ஒரு வரியிலிருந்து இன்னொன்றைக் கழிக்கவும், சில வரிகளை எண்ணால் பெருக்கவும் - அவ்வளவுதான்.

எனவே: இப்போது எல்லாம் ஒரே மாதிரியாக இருக்கும், ஆனால் ஒரு "வயது வந்தோர்" வழியில். தயாரா?

வரையறை. ஒரு அணி $A=\left[ n\times n \right]$ மற்றும் அதே அளவு $n$ என்ற அடையாள அணி $E$ கொடுக்கப்பட வேண்டும். பிறகு $\left[ A\left| இ\வலது. \right]$ என்பது $\left[ n\times 2n \right]$ அளவுள்ள புதிய அணி இது போல் தெரிகிறது:

\[\left[ A\left| இ\வலது. \right]=\left[ \begin(array)(rrrr|rrrr)((a)_(11)) & ((a)_(12)) & ... & ((a)_(1n)) & 1 & 0 & ... & 0 \\((a)_(21)) & ((a)_(22)) & ... & ((a)_(2n)) & 0 & 1 & ... & 0 \\... & ... & ... & ... & ... & ... & ... & ... \\((a)_(n1)) & ((a)_(n2)) & ... & ((a)_(nn)) & 0 & 0 & ... & 1 \\\ end(array) \right]\]

சுருக்கமாக, நாங்கள் $A$ என்ற மேட்ரிக்ஸை எடுத்துக்கொள்கிறோம், வலதுபுறத்தில் அதற்குத் தேவையான அளவு $E$ என்ற அடையாள அணியை ஒதுக்குகிறோம், அழகுக்காக செங்குத்துப் பட்டியில் அவற்றைப் பிரிக்கிறோம் - இங்கே உங்களுக்கு இணைப்பு உள்ளது. :)

என்ன பிடிப்பு? இதோ என்ன:

தேற்றம். அணி $A$ தலைகீழாக இருக்கட்டும். $\left[ A\left| இ\வலது. \right]$. பயன்படுத்தினால் அடிப்படை சரம் மாற்றங்கள்$\left[ E\left| வடிவத்திற்கு கொண்டு வாருங்கள் பிரகாசமான. \right]$, அதாவது. $A$ இலிருந்து வலதுபுறத்தில் உள்ள அணி $E$ ஐப் பெற வரிசைகளைப் பெருக்கி, கழித்தல் மற்றும் மறுசீரமைப்பதன் மூலம், இடதுபுறத்தில் பெறப்பட்ட $B$ அணி $A$ இன் தலைகீழ் ஆகும்:

\[\left[ A\left| இ\வலது. \right]\to \left[ E\left| பிரகாசமான. \right]\Rightarrow B=((A)^(-1))\]

இது மிகவும் எளிமையானது! சுருக்கமாக, தலைகீழ் மேட்ரிக்ஸைக் கண்டறிவதற்கான அல்காரிதம் இதுபோல் தெரிகிறது:

$\left[ A\left| என்ற இணை அணியை எழுதவும் இ\வலது. \right]$;
$A$ க்குப் பதிலாக $E$ தோன்றும் வரை அடிப்படை சரம் மாற்றங்களைச் செய்யவும்;
நிச்சயமாக, இடதுபுறத்திலும் ஏதாவது தோன்றும் - ஒரு குறிப்பிட்ட அணி $B$. இது எதிர்மாறாக இருக்கும்;
லாபம்! :)

நிச்சயமாக, இதைச் சொல்வதை விட இது மிகவும் எளிதானது. எனவே ஓரிரு உதாரணங்களைப் பார்ப்போம்: $\left[ 3\times 3 \right]$ மற்றும் $\left[ 4\time 4 \right]$ அளவுகளுக்கு.

பணி. தலைகீழ் மேட்ரிக்ஸைக் கண்டறியவும்:

\[\left[ \begin(array)(*(35)(r)) 1 & 5 & 1 \\ 3 & 2 & 1 \\ 6 & -2 & 1 \\\ end(array) \right]\ ]

தீர்வு. நாங்கள் இணை அணியை உருவாக்குகிறோம்:

\[\left[ \begin(array)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 3 & 2 & 1 & 0 & 1 & 0 \\ 6 & -2 & 1 & 0 & 0 & 1 \\\ முடிவு(வரிசை) \வலது]\]

அசல் மேட்ரிக்ஸின் கடைசி நெடுவரிசை ஒன்று நிரப்பப்பட்டிருப்பதால், மற்றவற்றிலிருந்து முதல் வரிசையைக் கழிக்கவும்:

\[\begin(align) & \left[ \begin(array)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 3 & 2 & 1 & 0 & 1 & 0 \\ 6 & - 2 & 1 & 0 & 0 & 1 \\\ முடிவு(வரிசை) \வலது]\ஆரம்பம்(மேட்ரிக்ஸ்) \\\\ [ \begin(array)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 5 & -7 & 0 & -1 & 0 & 1 \\\ end(array) \right] \\ \end(align)\]

முதல் வரியைத் தவிர வேறு அலகுகள் இல்லை. ஆனால் நாங்கள் அதைத் தொடவில்லை, இல்லையெனில் புதிதாக அகற்றப்பட்ட அலகுகள் மூன்றாவது நெடுவரிசையில் "பெருக்க" தொடங்கும்.

ஆனால் இரண்டாவது வரியை கடைசியிலிருந்து இரண்டு முறை கழிக்கலாம் - கீழ் இடது மூலையில் ஒன்றைப் பெறுகிறோம்:

\[\begin(align) & \left[ \begin(array)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 5 & -7 & 0 & -1 & 0 & 1 \\\ end(array) \right]\begin(matrix) \ \\ \downarrow \\ -2 \\\ end(matrix)\ to \\ & \left [ \begin(array)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\ end(array) \right] \\ \end(align)\]

இப்போது நாம் கடைசி வரிசையை முதல் மற்றும் இரண்டு முறை இரண்டிலிருந்து கழிக்கலாம் - இந்த வழியில் நாம் முதல் நெடுவரிசையை "பூஜ்ஜியம்" செய்கிறோம்:

\[\begin(align) & \left[ \begin(array)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\ end(array) \right]\begin(matrix) -1 \\ -2 \\ \uparrow \\\ end(matrix)\to \\ & \ \இடதுபுறம்[ \begin(array)(rrr|rrr) 0 & 6 & 1 & 0 & 2 & -1 \\ 0 & -1 & 0 & -3 & 5 & -2 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\ முடிவு(வரிசை) \வலது] \\ \முடிவு(சீரமைப்பு)\]

இரண்டாவது வரியை −1 ஆல் பெருக்கவும், பின்னர் அதை முதல் வரியிலிருந்து 6 முறை கழித்து கடைசியில் 1 முறை சேர்க்கவும்:

\[\begin(align) & \left[ \begin(array)(rrr|rrr) 0 & 6 & 1 & 0 & 2 & -1 \\ 0 & -1 & 0 & -3 & 5 & -2 \ \ 1 & -1 & 0 & 1 & -2 & 1 \\\ முடிவு(வரிசை) \ right]\begin(matrix) \ \\ \left| \cdot \left(-1 \right) \right. \\ \ \\\ end(matrix)\to \\ & \\to \left[ \begin(array)(rrr|rrr) 0 & 6 & 1 & 0 & 2 & -1 \\ 0 & 1 & 0 & 3 & -5 & 2 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\ முடிவு(வரிசை) \right]\begin(matrix) -6 \\ \updownarrow \\ +1 \\\ end அணி \\ 1 & 0 & 0 & 4 & -7 & 3 \\\ முடிவு(வரிசை) \ right] \\ \ end(align)\]

1 மற்றும் 3 வரிகளை மாற்றுவது மட்டுமே மீதமுள்ளது:

\[\left[ \begin(array)(rrr|rrr) 1 & 0 & 0 & 4 & -7 & 3 \\ 0 & 1 & 0 & 3 & -5 & 2 \\ 0 & 0 & 1 & - 18 & 32 & -13 \\\ முடிவு(வரிசை) \வலது]\]

தயார்! வலதுபுறத்தில் தேவையான தலைகீழ் அணி உள்ளது.

பதில். $\left[ \begin(array)(*(35)(r))4 & -7 & 3 \\ 3 & -5 & 2 \\ -18 & 32 & -13 \\\ end(array) \right ]$

பணி. தலைகீழ் மேட்ரிக்ஸைக் கண்டறியவும்:

\[\left[ \begin(matrix) 1 & 4 & 2 & 3 \\ 1 & -2 & 1 & -2 \\ 1 & -1 & 1 & 1 \\ 0 & -10 & -2 & -5 \\\ முடிவு(மேட்ரிக்ஸ்) \வலது]\]

தீர்வு. நாங்கள் மீண்டும் இணைப்பினை உருவாக்குகிறோம்:

\[\left[ \begin(array)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 1 & -2 & 1 & -2 & 0 & 1 & 0 & 0 \ \ 1 & -1 & 1 & 1 & 0 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\\ முடிவு(வரிசை) \right]\]

கொஞ்சம் அழுவோம், இனி எவ்வளவு எண்ண வேண்டியிருக்கிறது என்று வருத்தமாக இருங்கள்... எண்ணத் தொடங்குங்கள். முதலில், வரிசை 2 மற்றும் 3 இலிருந்து வரிசை 1 ஐக் கழிப்பதன் மூலம் முதல் நெடுவரிசையை "பூஜ்ஜியமாக" செய்வோம்:

\[\begin(align) & \left[ \begin(array)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 1 & -2 & 1 & -2 & 0 & 1 & 0 & 0 \\ 1 & -1 & 1 & 1 & 0 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\\ முடிவு(வரிசை) \right]\begin(matrix) \downarrow \\ -1 \\ -1 \\ \ \\\ end(matrix)\to \\ & \\ to \left[ \begin(array)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 0 & -6 & -1 & -5 & -1 & 1 & 0 & 0 \\ 0 & -5 & -1 & -2 & -1 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\\ முடிவு(வரிசை) \ right] \\ \ end(align)\]

2-4 வரிகளில் பல "தீமைகளை" காண்கிறோம். மூன்று வரிசைகளையும் −1 ஆல் பெருக்கவும், பின்னர் வரிசை 3 ஐ மற்றவற்றிலிருந்து கழிப்பதன் மூலம் மூன்றாவது நெடுவரிசையை எரிக்கவும்:

\[\begin(align) & \left[ \begin(array)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 0 & -6 & -1 & -5 & - 1 & 1 & 0 & 0 \\ 0 & -5 & -1 & -2 & -1 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\ \end(array) \right]\begin(matrix) \ \\ \left| \cdot \left(-1 \right) \right. \\ \இடது| \cdot \left(-1 \right) \right. \\ \இடது| \cdot \left(-1 \right) \right. \\\ end(matrix)\to \\ & \\to \left[ \begin(array)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 0 & 6 & 1 & 5 & 1 & -1 & 0 & 0 \\ 0 & 5 & 1 & 2 & 1 & 0 & -1 & 0 \\ 0 & 10 & 2 & 5 & 0 & 0 & 0 & -1 \\ \end (array) \right]\begin(matrix) -2 \\ -1 \\ \updownarrow \\ -2 \\\ end(matrix)\ to \\ & \\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\ rrrr| rrrr) 1 & -6 & 0 & -1 & -1 & 0 & 2 & 0 \\ 0 & 1 & 0 & 3 & 0 & -1 & 1 & 0 \\ 0 & 5 & 1 & 2 & 1 & 0 & -1 & 0 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\ முடிவு(வரிசை) \ right] \\ \ end(align)\]

அசல் மேட்ரிக்ஸின் கடைசி நெடுவரிசையை "வறுக்க" இப்போது நேரம் வந்துவிட்டது: மீதமுள்ளவற்றிலிருந்து வரிசை 4 ஐக் கழிக்கவும்:

\[\begin(align) & \left[ \begin(array)(rrrr|rrrr) 1 & -6 & 0 & -1 & -1 & 0 & 2 & 0 \\ 0 & 1 & 0 & 3 & 0 & -1 & 1 & 0 \\ 0 & 5 & 1 & 2 & 1 & 0 & -1 & 0 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\ முடிவு(வரிசை ) \right]\begin(matrix) +1 \\ -3 \\ -2 \\ \uparrow \\\ end(matrix)\to \\ & \\ to \left[ \begin(array)(rrrr|rrrr) 1 & -6 & 0 & 0 & -3 & 0 & 4 & -1 \\ 0 & 1 & 0 & 0 & 6 & -1 & -5 & 3 \\ 0 & 5 & 1 & 0 & 5 & 0 & -5 & 2 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\ end(array) \right] \\ \end(align)\]

இறுதி எறிதல்: வரி 1 மற்றும் 3 இலிருந்து வரி 2 ஐக் கழிப்பதன் மூலம் இரண்டாவது நெடுவரிசையை "எரிக்கவும்":

\[\begin(align) & \left[ \begin(array)(rrrr|rrrr) 1 & -6 & 0 & 0 & -3 & 0 & 4 & -1 \\ 0 & 1 & 0 & 0 & 6 & -1 & -5 & 3 \\ 0 & 5 & 1 & 0 & 5 & 0 & -5 & 2 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\ முடிவு( வரிசை) \right]\begin(matrix) 6 \\ \updownarrow \\ -5 \\ \ \\\ end(matrix)\to \\ & \\to \left[ \begin(array)(rrrr|rrrr) 1 & 0 & 0 & 0 & 33 & -6 & -26 & -17 \\ 0 & 1 & 0 & 0 & 6 & -1 & -5 & 3 \\ 0 & 0 & 1 & 0 & -25 & 5 & 20 & -13 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\ முடிவு(வரிசை) \ right] \\ \ end(align)\]

மீண்டும் அடையாள அணி இடதுபுறத்தில் உள்ளது, அதாவது தலைகீழ் வலதுபுறத்தில் உள்ளது. :)

பதில். $\left[ \begin(matrix) 33 & -6 & -26 & 17 \\ 6 & -1 & -5 & 3 \\ -25 & 5 & 20 & -13 \\ -2 & 0 & 2 & - 1 \\\ முடிவு(மேட்ரிக்ஸ்) \right]$

சரி இப்போது எல்லாம் முடிந்துவிட்டது. நீங்களே சரிபார்த்துக் கொள்ளுங்கள் - நான் ஏமாற்றப்பட்டேன். :)

பல பண்புகளில் தலைகீழ் போன்றது.

என்சைக்ளோபீடிக் YouTube

1 / 5

✪ தலைகீழ் அணி (கண்டுபிடிப்பதற்கான 2 வழிகள்)

✪ ஒரு அணி - bezbotvy இன் தலைகீழ் எவ்வாறு கண்டுபிடிப்பது

✪ தலைகீழ் அணி #1

✪ தலைகீழ் மேட்ரிக்ஸ் முறையைப் பயன்படுத்தி சமன்பாடுகளின் அமைப்பைத் தீர்ப்பது - bezbotvy

✪ தலைகீழ் அணி

வசன வரிகள்

தலைகீழ் மேட்ரிக்ஸின் பண்புகள்

det A - 1 = 1 det A (\டிஸ்ப்ளேஸ்டைல் \det A^(-1)=(\frac (1)(\det A))), எங்கே det (\Displaystyle \\det)தீர்மானிப்பதைக் குறிக்கிறது.
(A B) − 1 = B - 1 A - 1 (\டிஸ்ப்ளே ஸ்டைல் \ (AB)^(-1)=B^(-1)A^(-1))இரண்டு சதுர தலைகீழ் மெட்ரிக்குகளுக்கு A (\டிஸ்ப்ளேஸ்டைல் A)மற்றும் பி (\டிஸ்ப்ளேஸ்டைல் பி).
(A T) − 1 = (A - 1) T (\டிஸ்ப்ளேஸ்டைல் \ (A^(T))^(-1)=(A^(-1))^(T)), எங்கே (.. .) டி (\டிஸ்ப்ளேஸ்டைல் (...)^(டி))ஒரு இடமாற்ற அணியைக் குறிக்கிறது.
(k A) − 1 = k - 1 A - 1 (\டிஸ்ப்ளே ஸ்டைல் \ (kA)^(-1)=k^(-1)A^(-1))எந்த குணகத்திற்கும் k ≠ 0 (\டிஸ்ப்ளே ஸ்டைல் k\not =0).
E - 1 = E (\டிஸ்ப்ளேஸ்டைல் \E^(-1)=E).
நேரியல் சமன்பாடுகளின் அமைப்பைத் தீர்க்க வேண்டிய அவசியம் ஏற்பட்டால், (b என்பது பூஜ்ஜியமற்ற திசையன்) எங்கே x (\டிஸ்ப்ளே ஸ்டைல் x)விரும்பிய திசையன், மற்றும் என்றால் A - 1 (\டிஸ்ப்ளே ஸ்டைல் A^(-1))உள்ளது, பின்னர் x = A - 1 b (\displaystyle x=A^(-1)b). இல்லையெனில், தீர்வு இடத்தின் பரிமாணம் பூஜ்ஜியத்தை விட அதிகமாக இருக்கும், அல்லது தீர்வுகள் எதுவும் இல்லை.

தலைகீழ் மேட்ரிக்ஸைக் கண்டறிவதற்கான முறைகள்

அணி தலைகீழாக இருந்தால், தலைகீழ் மேட்ரிக்ஸைக் கண்டுபிடிக்க நீங்கள் பின்வரும் முறைகளில் ஒன்றைப் பயன்படுத்தலாம்:

சரியான (நேரடி) முறைகள்

காஸ்-ஜோர்டான் முறை

இரண்டு மெட்ரிக்குகளை எடுத்துக் கொள்வோம்: தி ஏமற்றும் ஒற்றை ஈ. மேட்ரிக்ஸை முன்வைப்போம் ஏகாஸ்-ஜோர்டான் முறையைப் பயன்படுத்தி அடையாள அணிக்கு, வரிசைகளில் உருமாற்றங்களைப் பயன்படுத்துதல் (நீங்கள் நெடுவரிசைகளிலும் மாற்றங்களைப் பயன்படுத்தலாம், ஆனால் ஒன்றுக்கொன்று அல்ல). ஒவ்வொரு செயல்பாட்டையும் முதல் மேட்ரிக்ஸில் பயன்படுத்திய பிறகு, அதே செயல்பாட்டை இரண்டாவது அணிக்கும் பயன்படுத்தவும். முதல் மேட்ரிக்ஸை யூனிட் வடிவமாகக் குறைப்பது முடிந்ததும், இரண்டாவது மேட்ரிக்ஸ் சமமாக இருக்கும் A−1.

காஸியன் முறையைப் பயன்படுத்தும் போது, முதல் அணி இடதுபுறத்தில் உள்ள ஒரு அடிப்படை மெட்ரிக்ஸால் பெருக்கப்படும். Λ i (\டிஸ்ப்ளேஸ்டைல் \Lambda _(i))(ஒரு நிலையைத் தவிர, பிரதான மூலைவிட்டத்தில் அலகுகளைக் கொண்ட இடமாற்றம் அல்லது மூலைவிட்ட அணி):

Λ 1 ⋅ ⋯ ⋅ Λ n ⋅ A = Λ A = E ⇒ Λ = A − 1 (\Displaystyle \Lambda _(1)\cdot \dots \cdot \Lambda _(n)\cdot A=\Elamb \Rightarrow \Lambda =A^(-1)). Λ m = [ 1 ... 0 - a 1 m / a m 0 … 0 … 0 … 1 - a m - 1 m / a m m 0 ... 0 0 … 0 1 / a m m 0 … 0 0 … 0 − a m + 1 m / a m … 0 … 0 … 0 - a n m / a m 0 … 1 ] (\displaystyle \Lambda _(m)=(\begin(bmatrix)1&\ dots &0&-a_(1m)/a_(mm)&0&\ dots &0\\ &&&\ புள்ளிகள் &&&\\0&\ புள்ளிகள் &1&-a_(m-1m)/a_(mm)&0&\ dots &0\\0&\ dots &0&1/a_(mm)&0&\ dots &0\\0&\ dots &0&-a_( m+1m)/a_(mm)&1&\dts &0\\&&&\dts &&&\\0&\ dots &0&-a_(nm)/a_(mm)&0&\ dots &1\end(bmatrix))).

அனைத்து செயல்பாடுகளையும் பயன்படுத்திய பிறகு இரண்டாவது மேட்ரிக்ஸ் சமமாக இருக்கும் Λ (\டிஸ்ப்ளே ஸ்டைல் \ லாம்ப்டா), அதாவது, அது விரும்பிய ஒன்றாக இருக்கும். அல்காரிதம் சிக்கலானது - O (n 3) (\டிஸ்ப்ளே ஸ்டைல் O(n^(3))).

இயற்கணித நிரப்பு அணியைப் பயன்படுத்துதல்

மேட்ரிக்ஸின் தலைகீழ் அணி A (\டிஸ்ப்ளேஸ்டைல் A), வடிவத்தில் குறிப்பிடலாம்

A − 1 = adj (A) det (A) (\displaystyle (A)^(-1)=(((\mbox(adj))(A)) \over (\det(A))))

எங்கே adj (A) (\displaystyle (\mbox(adj))(A))- இணை அணி;

அல்காரிதத்தின் சிக்கலானது, O det ஐக் கணக்கிடுவதற்கான அல்காரிதத்தின் சிக்கலைச் சார்ந்தது மற்றும் O(n²)·O det க்கு சமம்.

LU/LUP சிதைவைப் பயன்படுத்துதல்

மேட்ரிக்ஸ் சமன்பாடு A X = I n (\displaystyle AX=I_(n))தலைகீழ் அணிக்கு எக்ஸ் (\டிஸ்ப்ளேஸ்டைல் எக்ஸ்)தொகுப்பாகக் கருதலாம் n (\displaystyle n)படிவத்தின் அமைப்புகள் A x = b (\displaystyle Ax=b). குறிப்போம் i (\டிஸ்ப்ளே ஸ்டைல் i)மேட்ரிக்ஸின் வது நெடுவரிசை எக்ஸ் (\டிஸ்ப்ளேஸ்டைல் எக்ஸ்)மூலம் X i (\டிஸ்ப்ளே ஸ்டைல் X_(i)); பிறகு A X i = e i (\displaystyle AX_(i)=e_(i)), i = 1 , … , n (\ displaystyle i=1,\ldots ,n),ஏனெனில் i (\டிஸ்ப்ளே ஸ்டைல் i)மேட்ரிக்ஸின் வது நெடுவரிசை I n (\displaystyle I_(n))அலகு திசையன் ஆகும் e i (\displaystyle e_(i)). வேறு வார்த்தைகளில் கூறுவதானால், தலைகீழ் மேட்ரிக்ஸைக் கண்டறிவது, அதே அணி மற்றும் வெவ்வேறு வலது பக்கங்களுடன் n சமன்பாடுகளைத் தீர்க்கும். LUP சிதைவைச் செய்த பிறகு (O(n³) நேரம்), n சமன்பாடுகள் ஒவ்வொன்றையும் தீர்க்க O(n²) நேரம் எடுக்கும், எனவே வேலையின் இந்தப் பகுதிக்கும் O(n³) நேரம் தேவைப்படுகிறது.

அணி A ஒருமையல்லாததாக இருந்தால், அதற்கு LUP சிதைவைக் கணக்கிடலாம் P A = L U (\displaystyle PA=LU). விடுங்கள் P A = B (\displaystyle PA=B), B - 1 = D (\டிஸ்ப்ளே ஸ்டைல் B^(-1)=D). தலைகீழ் மேட்ரிக்ஸின் பண்புகளிலிருந்து நாம் எழுதலாம்: D = U - 1 L - 1 (\டிஸ்ப்ளே ஸ்டைல் D=U^(-1)L^(-1)). இந்த சமத்துவத்தை U மற்றும் L ஆல் பெருக்கினால், படிவத்தின் இரண்டு சமத்துவங்களைப் பெறலாம் U D = L - 1 (\displaystyle UD=L^(-1))மற்றும் DL = U - 1 (\டிஸ்ப்ளே ஸ்டைல் DL=U^(-1)). இந்த சமத்துவங்களில் முதலாவது n² நேரியல் சமன்பாடுகளின் அமைப்பாகும் n (n + 1) 2 (\டிஸ்ப்ளேஸ்டைல் (\frac (n(n+1))(2)))அதில் இருந்து வலது பக்கங்கள் அறியப்படுகின்றன (முக்கோண மெட்ரிக்குகளின் பண்புகளிலிருந்து). இரண்டாவது n² நேரியல் சமன்பாடுகளின் அமைப்பையும் குறிக்கிறது n (n - 1) 2 (\டிஸ்ப்ளேஸ்டைல் (\frac (n(n-1))(2)))இதிலிருந்து வலது பக்கங்கள் அறியப்படுகின்றன (முக்கோண மெட்ரிக்குகளின் பண்புகளிலிருந்தும்). அவை ஒன்றாக n² சமத்துவ அமைப்பைக் குறிக்கின்றன. இந்த சமத்துவங்களைப் பயன்படுத்தி, அணி D இன் அனைத்து n² உறுப்புகளையும் நாம் மீண்டும் மீண்டும் தீர்மானிக்க முடியும். பின்னர் சமத்துவத்திலிருந்து (PA) −1 = A -1 P -1 = B -1 = D. சமத்துவத்தைப் பெறுகிறோம். A - 1 = D P (\displaystyle A^(-1)=DP).

LU சிதைவைப் பயன்படுத்தும் விஷயத்தில், அணி D இன் நெடுவரிசைகளின் வரிசைமாற்றம் தேவையில்லை, ஆனால் அணி A தனித்தன்மையற்றதாக இருந்தாலும் தீர்வு வேறுபடலாம்.

அல்காரிதத்தின் சிக்கலானது O(n³) ஆகும்.

மீண்டும் மீண்டும் செய்யும் முறைகள்

ஷூல்ட்ஸ் முறைகள்

( Ψ k = E - A U k , U k + 1 = U k ∑ i = 0 n Ψ k i (\displaystyle (\begin(cases)\Psi _(k)=E-AU_(k),\\U_( k+1)=U_(k)\sum _(i=0)^(n)\Psi _(k)^(i)\end(cases)))

பிழை மதிப்பீடு

ஆரம்ப தோராயத்தைத் தேர்ந்தெடுப்பது

இங்கே பரிசீலிக்கப்படும் மறுசெயல் மேட்ரிக்ஸ் தலைகீழ் செயல்முறைகளில் ஆரம்ப தோராயத்தைத் தேர்ந்தெடுப்பதில் உள்ள சிக்கல், எடுத்துக்காட்டாக, மெட்ரிக்குகளின் LU சிதைவின் அடிப்படையில் நேரடி தலைகீழ் முறைகளுடன் போட்டியிடும் சுயாதீன உலகளாவிய முறைகளாக அவற்றைக் கருத அனுமதிக்காது. தேர்வு செய்ய சில பரிந்துரைகள் உள்ளன U 0 (\டிஸ்ப்ளே ஸ்டைல் U_(0)), நிபந்தனையின் நிறைவேற்றத்தை உறுதி செய்தல் ρ (Ψ 0) < 1 {\displaystyle \rho (\Psi _{0})<1} (மேட்ரிக்ஸின் நிறமாலை ஆரம் ஒற்றுமையை விட குறைவாக உள்ளது), இது செயல்முறையின் ஒருங்கிணைப்புக்கு அவசியமானது மற்றும் போதுமானது. இருப்பினும், இந்த விஷயத்தில், முதலில், தலைகீழான அணி A அல்லது மேட்ரிக்ஸின் ஸ்பெக்ட்ரம் மதிப்பீட்டிற்கு மேலே இருந்து தெரிந்து கொள்ள வேண்டும். A A T (\டிஸ்ப்ளே ஸ்டைல் AA^(T))(அதாவது, A என்பது சமச்சீர் நேர்மறை திட்டவட்ட அணி மற்றும் ρ (A) ≤ β (\டிஸ்ப்ளேஸ்டைல் \rho (A)\leq \beta ), பிறகு நீங்கள் எடுக்கலாம் U 0 = α E (\displaystyle U_(0)=(\alpha )E), எங்கே ; A என்பது தன்னிச்சையான ஒருமை அல்லாத அணி மற்றும் ρ (A A T) ≤ β (\டிஸ்ப்ளேஸ்டைல் \rho (AA^(T))\leq \beta ), பின்னர் அவர்கள் நம்புகிறார்கள் U 0 = α A T (\displaystyle U_(0)=(\alpha )A^(T)), எங்கேயும் α ∈ (0 , 2 β) (\ டிஸ்ப்ளேஸ்டைல் \alpha \in \\இடது(0,(\frac (2)(\beta ))\வலது)); நீங்கள் நிச்சயமாக, நிலைமையை எளிதாக்கலாம் மற்றும் அதைப் பயன்படுத்திக் கொள்ளலாம் ρ (A A T) ≤ k A A T k (\டிஸ்ப்ளேஸ்டைல் \rho (AA^(T))\leq (\mathcal (k))AA^(T)(\mathcal (k))), போடு U 0 = A T‖ A A T‖ (\displaystyle U_(0)=(\frac (A^(T))(\|AA^(T)\|)))) இரண்டாவதாக, இந்த வழியில் ஆரம்ப மேட்ரிக்ஸைக் குறிப்பிடும்போது, அதற்கு எந்த உத்தரவாதமும் இல்லை ‖ Ψ 0 ‖ (\டிஸ்ப்ளேஸ்டைல் \|\Psi _(0)\|)சிறியதாக இருக்கும் (ஒருவேளை அது கூட மாறிவிடும் ‖ Ψ 0 ‖ > 1 (\displaystyle \|\Psi _(0)\|>1)), மற்றும் குவிதல் விகிதத்தின் உயர் வரிசை உடனடியாக வெளிப்படுத்தப்படாது.

எடுத்துக்காட்டுகள்

அணி 2x2

வெளிப்பாட்டைப் பாகுபடுத்த முடியவில்லை (தொடரியல் பிழை): (\displaystyle \mathbf(A)^(-1) = \begin(bmatrix) a & b \\ c & d \\ \end(bmatrix)^(-1) = \ frac (1)(\det(\mathbf(A))) \begin& \!\!-b \\ -c & \,a \\ \end(bmatrix) = \frac(1)(ad - bc) \ ஆரம்பம் (bmatrix) \,\,\,d & \!\!-b\\ -c & \,a \\ \end(bmatrix))

2x2 மேட்ரிக்ஸின் தலைகீழ் மாற்றமானது நிபந்தனையின் கீழ் மட்டுமே சாத்தியமாகும் a d − b c = det A ≠ 0 (\displaystyle ad-bc=\det A\neq 0).

நேரியல் சமன்பாடுகளின் அமைப்பைத் தீர்க்க (3) பொறுத்து x 1காசியன் முறையைப் பயன்படுத்துவோம்.

நேரியல் சமன்பாடுகளின் மீதமுள்ள அமைப்புகள் (2) இதே வழியில் தீர்க்கப்படுகின்றன.

இறுதியாக நெடுவரிசை திசையன்களின் குழு x 1 , x 2 , ..., x nதலைகீழ் அணியை உருவாக்குகிறது A-1.

ஒருமுறை வரிசைமாற்ற மெட்ரிக்குகளைக் கண்டறிவது என்பதை நினைவில் கொள்ளவும் P 1 , P 2 , ... , P n-1மற்றும் விதிவிலக்கு மெட்ரிக்குகள் M 1, M 2, ..., M n-1(பக்கம் காசியன் நீக்குதல் முறையைப் பார்க்கவும்) மற்றும் மேட்ரிக்ஸை உருவாக்குதல்

M=M n-1 P n-1 ...M 2 P 2 M 1 P 1 ,

அமைப்பு (2) வடிவத்திற்கு மாற்றப்படலாம்

அதிகபட்சம் 1 = நான் 1,
அதிகபட்சம் 2 = நான் 2,
......
MAx n =Me n.

இங்கிருந்து x 1 ,x 2 , ..., x n, வெவ்வேறு வலது பக்கங்களுடன் Me 1, Me 2, ..., Me n.

தலைகீழ் மேட்ரிக்ஸைக் கணக்கிடும்போது, அசல் மேட்ரிக்ஸின் வலது பக்கத்தில் அடையாள அணியைச் சேர்ப்பது மிகவும் வசதியானது மற்றும் முன்னோக்கி மற்றும் பின்தங்கிய திசைகளில் காஸியன் முறையைப் பயன்படுத்துகிறது.

இதை ஒரு உதாரணத்துடன் பார்க்கலாம்.