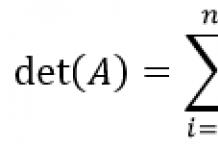Matritsaning elementlarga parchalanishi. Matritsa determinanti. Determinant uchun formulalar

Ta'rif 1. 7. Kichik determinant elementi - tanlangan element paydo bo'lgan satr va ustunni kesib tashlash orqali berilgan elementdan olingan aniqlovchi.

Belgilanish: aniqlovchining tanlangan elementi, uning kichikligi.

Misol. Uchun

Ta'rif 1. 8. Algebraik to‘ldiruvchi determinantning elementi, agar bu elementning indekslari yig'indisi i+j bo'lsa, uning kichiki deyiladi, agar i+j toq bo'lsa, minorga qarama-qarshi bo'lgan son, ya'ni.

Uchinchi darajali determinantlarni hisoblashning yana bir usulini ko'rib chiqaylik - satr yoki ustunni kengaytirish. Buning uchun quyidagi teoremani isbotlaymiz:

1.1 teorema. Aniqlovchi uning har qanday satrlari yoki ustunlari elementlari va ularning algebraik to'ldiruvchilari mahsuloti yig'indisiga teng, ya'ni.

bu yerda i=1,2,3.

Isbot.

Determinantning birinchi qatori uchun teoremani isbotlaylik, chunki boshqa har qanday satr yoki ustun uchun biz shunga o'xshash mulohaza yuritishimiz va bir xil natijani olishimiz mumkin.

Birinchi qator elementlariga algebraik to‘ldiruvchilarni topamiz:

Shunday qilib, determinantni hisoblash uchun har qanday satr yoki ustunning elementlariga algebraik to'ldiruvchilarni topish va determinantning mos keladigan elementlari bo'yicha ularning hosilalari yig'indisini hisoblash kifoya.

Misol. Birinchi ustunda kengaytirish yordamida determinantni hisoblaymiz. E'tibor bering, bu holda qidirishning hojati yo'q, chunki biz topamiz va Demak,

Yuqori darajalarni belgilovchi omillar.

Ta'rif 1. 9. n-tartib aniqlovchi

n summasi bor! a'zolari ularning har biri n dan biriga mos keladi! 1,2,…,n to‘plamdagi elementlarning r juft almashinishi orqali olingan tartiblangan to‘plamlar.

Izoh 1. 3-tartib aniqlovchilarning xossalari n-tartibli aniqlovchilar uchun ham amal qiladi.

Izoh 2. Amalda yuqori tartiblarning determinantlari qator yoki ustunni kengaytirish yordamida hisoblanadi. Bu bizga hisoblangan determinantlar tartibini pasaytirish va oxir-oqibat uchinchi darajali determinantlarni topish muammosini kamaytirish imkonini beradi.

Misol. 4-tartibli determinantni hisoblaymiz 2-ustun bo'ylab kengaytirish yordamida. Buning uchun biz topamiz:

Demak,

Laplas teoremasi- chiziqli algebra teoremalaridan biri. U frantsuz matematigi Per-Simon Laplas (1749 - 1827) sharafiga nomlangan bo'lib, u 1772 yilda ushbu teoremani shakllantirishga hissa qo'shgan, garchi bu teoremaning alohida holati Leybnitsga determinantning ketma-ket (ustun) bo'linishi bo'yicha ma'lum bo'lgan. .

vayronagarchilik minor quyidagicha ta'riflanadi:

Quyidagi bayonot haqiqatdir.

Laplas teoremasida yig'indi olinadigan kichiklar soni ustunlarni tanlash usullari soniga, ya'ni binom koeffitsientiga teng.

Matritsaning satrlari va ustunlari determinantning xususiyatlariga nisbatan ekvivalent bo'lganligi sababli, matritsa ustunlari uchun Laplas teoremasini shakllantirish mumkin.

Aniqlovchining qatorga (ustun) kengayishi (Xulosa 1)

Laplas teoremasining keng tarqalgan maxsus holati determinantning qator yoki ustundagi kengayishidir. U kvadrat matritsaning determinantini uning istalgan satrlari yoki ustunlari elementlari va ularning algebraik toʻldiruvchilari mahsuloti yigʻindisi sifatida koʻrsatish imkonini beradi.

O'lchamli kvadrat matritsa bo'lsin. Shuningdek, matritsaning qator yoki ustun raqami ham berilsin. Keyin determinantni quyidagi formulalar yordamida hisoblash mumkin.

Keyingi xususiyatlar kichik va algebraik to'ldiruvchi tushunchalari bilan bog'liq

Kichik element determinant deb ataladi, bu element ushbu element joylashgan kesishgan satr va ustunni kesib o'tgandan keyin qolgan elementlardan iborat. Tartib determinantining kichik elementi tartibga ega. Biz uni bilan belgilaymiz.

1-misol. Mayli , Keyin .

Bu minor A dan ikkinchi qator va uchinchi ustunni kesib tashlash orqali olinadi.

Algebraik to‘ldiruvchi elementga ko'paytiriladigan mos keladigan minor deyiladi, ya'ni. , qayerda bu element joylashgan chorrahadagi satr va ustunning soni.

VIII.(Aniqlovchining ma'lum bir qator elementlariga parchalanishi). Aniqlovchi ma'lum bir qator elementlari va ularga mos keladigan algebraik to'ldiruvchilarning ko'paytmalari yig'indisiga teng.

2-misol. Mayli , Keyin

3-misol. Matritsaning determinantini topamiz , uni birinchi qatorning elementlariga parchalash.

Rasmiy ravishda, bu teorema va determinantlarning boshqa xossalari faqat uchinchi tartibdan yuqori bo'lmagan matritsalar determinantlari uchun amal qiladi, chunki biz boshqa determinantlarni ko'rib chiqmadik. Quyidagi ta'rif bizga ushbu xususiyatlarni har qanday tartibdagi determinantlarga kengaytirish imkonini beradi.

Matritsaning aniqlovchisi buyurtma- kengayish teoremasi va determinantlarning boshqa xossalarini ketma-ket qo'llash orqali hisoblangan son.

Hisob-kitoblarning natijasi yuqoridagi xususiyatlarning qo'llanilishi va qaysi qatorlar va ustunlar uchun tartibiga bog'liq emasligini tekshirishingiz mumkin. Ushbu ta'rifdan foydalanib, determinant yagona topiladi.

Garchi bu ta'rif determinantni topishning aniq formulasini o'z ichiga olmasa ham, uni quyi tartibli matritsalarning determinantlariga qisqartirish orqali topish imkonini beradi. Bunday ta'riflar deyiladi takrorlanuvchi.

4-misol. Determinantni hisoblang:

Faktorizatsiya teoremasi berilgan matritsaning istalgan satri yoki ustuniga qo'llanilishi mumkin bo'lsa-da, iloji boricha ko'proq nollarni o'z ichiga olgan ustun bo'ylab faktoringlar yordamida kamroq hisoblar olinadi.

Matritsa nol elementlarga ega emasligi sababli, biz ularni xususiyatdan foydalanib olamiz VII. Birinchi qatorni ketma-ket raqamlar bilan ko'paytiring va uni qatorlarga qo'shing va oling:

Olingan determinantni birinchi ustun bo'ylab kengaytiramiz va quyidagilarni olamiz:

chunki determinant ikkita proportsional ustunni o'z ichiga oladi.

Matritsalarning ayrim turlari va ularning determinantlari

Asosiy diagonal () ostida yoki yuqorida nol elementga ega bo'lgan kvadrat matritsa deyiladi uchburchak.

Shunga ko'ra, ularning sxematik tuzilishi quyidagicha ko'rinadi: yoki

Oliy matematikada muammolarni hal qilishda ehtiyoj juda tez-tez paydo bo'ladi matritsaning determinantini hisoblang. Matritsaning determinanti chiziqli algebra, analitik geometriya, matematik tahlil va oliy matematikaning boshqa sohalarida uchraydi. Shunday qilib, determinantlarni echish mahoratisiz amalga oshirish mumkin emas. Shuningdek, o'z-o'zini sinab ko'rish uchun siz determinant kalkulyatorini bepul yuklab olishingiz mumkin, u sizga determinantlarni o'z-o'zidan echishni o'rgatmaydi, lekin bu juda qulay, chunki to'g'ri javobni oldindan bilish har doim foydalidir!

Men determinantning qat'iy matematik ta'rifini bermayman va umuman olganda, men matematik terminologiyani minimallashtirishga harakat qilaman; bu ko'pchilik o'quvchilar uchun osonlashtirmaydi. Ushbu maqolaning maqsadi sizga ikkinchi, uchinchi va to'rtinchi tartibli determinantlarni qanday hal qilishni o'rgatishdir. Barcha materiallar sodda va tushunarli shaklda taqdim etilgan va hatto oliy matematikada to'liq (bo'sh) choynak ham materialni diqqat bilan o'rgangandan so'ng, aniqlovchilarni to'g'ri hal qila oladi.

Amalda siz ko'pincha ikkinchi tartibli determinantni topishingiz mumkin, masalan: va uchinchi tartibli determinant, masalan: .

To'rtinchi tartibli determinant Bu ham antiqa narsa emas va biz unga dars oxirida erishamiz.

Umid qilamanki, hamma quyidagilarni tushunadi: Determinant ichidagi raqamlar o'z-o'zidan yashaydi va hech qanday ayirish haqida gap yo'q! Raqamlarni almashtirib bo'lmaydi!

(Xususan, determinantning satrlari yoki ustunlarini uning belgisini o'zgartirgan holda juftlik bilan qayta joylashtirishni amalga oshirish mumkin, lekin ko'pincha bu shart emas - keyingi darsga qarang: Determinantning xususiyatlari va tartibini pasaytiradi)

Shunday qilib, agar biron bir aniqlovchi berilgan bo'lsa, u holda Biz uning ichida hech narsaga tegmaymiz!

Belgilar: Agar matritsa berilgan bo'lsa , keyin uning determinanti belgilanadi. Bundan tashqari, ko'pincha determinant lotin harfi yoki yunoncha bilan belgilanadi.

1)Aniqlovchini yechish (topish, ochish) nimani anglatadi? Determinantni hisoblash RAQAMNI TOPISH demakdir. Yuqoridagi misollardagi savol belgilari butunlay oddiy sonlardir.

2) Endi aniqlash kerak Bu raqamni QANDAY topish mumkin? Buning uchun siz hozir muhokama qilinadigan muayyan qoidalar, formulalar va algoritmlarni qo'llashingiz kerak.

Keling, "ikki" ga "ikki" ning aniqlovchisidan boshlaylik.:

Buni hech bo'lmaganda universitetda oliy matematika bo'yicha o'qiyotganda eslash kerak.

Keling, darhol misolni ko'rib chiqaylik:

Tayyor. Eng muhimi, BELGILARDA CHALG'ILMASH.

Uch-uch matritsaning aniqlovchisi 8 ta usulda ochish mumkin, ulardan 2 tasi oddiy, 6 tasi normal.

Keling, ikkita oddiy usuldan boshlaylik

Ikki-ikki determinantga o'xshab, uch-uch determinantni quyidagi formula yordamida kengaytirish mumkin:

Formula uzoq va ehtiyotsizlik tufayli xato qilish oson. Qanday qilib zerikarli xatolardan qochish kerak? Shu maqsadda determinantni hisoblashning ikkinchi usuli ixtiro qilindi, bu aslida birinchisiga to'g'ri keladi. Bu Sarrus usuli yoki "parallel chiziqlar" usuli deb ataladi.
Xulosa shuki, determinantning o'ng tomonida birinchi va ikkinchi ustunlarni belgilang va diqqat bilan qalam bilan chiziqlar torting:

"Qizil" diagonallarda joylashgan ko'paytirgichlar "ortiqcha" belgisi bilan formulaga kiritilgan.
"Ko'k" diagonallarda joylashgan ko'paytirgichlar minus belgisi bilan formulaga kiritilgan:

Misol:

Ikki yechimni solishtiring. Bu xuddi shunday ekanligini ko'rish oson, faqat ikkinchi holatda formula omillari biroz o'zgartiriladi va eng muhimi, xato qilish ehtimoli ancha past bo'ladi.

Endi determinantni hisoblashning oltita normal usulini ko'rib chiqamiz

Nega normal? Chunki aksariyat hollarda saralovchilar shu tarzda oshkor etilishi kerak.

Siz sezganingizdek, uch-uch determinant uchta ustun va uchta qatorga ega.
Determinantni ochish orqali hal qilishingiz mumkin istalgan satr yoki ustun bo'yicha.
Shunday qilib, barcha holatlarda 6 ta usul mavjud bir xil turdagi algoritm.

Matritsaning determinanti qator (ustun) elementlarining tegishli algebraik to'ldiruvchilarning mahsuloti yig'indisiga teng. Qo'rqinchlimi? Hammasi ancha sodda, biz ilmiy bo'lmagan, ammo tushunarli yondashuvni qo'llaymiz, hatto matematikadan uzoq odamga ham kirish mumkin.

Keyingi misolda determinantni kengaytiramiz birinchi qatorda.
Buning uchun bizga belgilar matritsasi kerak: . Belgilar shaxmat taxtasi shaklida joylashtirilganini sezish oson.

Diqqat! Belgilar matritsasi mening shaxsiy ixtirom. Bu kontseptsiya ilmiy emas, uni topshiriqlarni yakuniy loyihalashda qo'llash shart emas, u faqat determinantni hisoblash algoritmini tushunishga yordam beradi.

Avval to'liq yechimni beraman. Biz yana eksperimental determinantimizni olamiz va hisob-kitoblarni bajaramiz:

Va asosiy savol: buni "uchdan uch" determinantidan QANDAY olish mumkin:
?

Shunday qilib, "uchdan uch" determinant uchta kichik determinantni echishga tushadi yoki ular ham deyiladi, MINOROV. Men atamani eslab qolishni maslahat beraman, ayniqsa esda qolarli: kichik - kichik.

Determinantning parchalanish usuli tanlangandan keyin birinchi qatorda, hamma narsa uning atrofida aylanishi aniq:

Elementlar odatda chapdan o'ngga (yoki ustun tanlangan bo'lsa, yuqoridan pastga) ko'riladi.

Keling, avval chiziqning birinchi elementi bilan, ya'ni bitta element bilan ishlaymiz:

1) Belgilar matritsasidan tegishli belgini yozamiz:

2) Keyin elementning o'zini yozamiz:

3) Birinchi element paydo bo'lgan qator va ustunni aqliy ravishda kesib tashlang:

Qolgan to'rtta raqam "ikkidan ikkiga" determinantni tashkil qiladi, bu chaqiriladi MINOR berilgan element (birlik).

Keling, chiziqning ikkinchi elementiga o'tamiz.

4) Belgilar matritsasidan tegishli belgini yozamiz:

5) Keyin ikkinchi elementni yozing:

6) Ikkinchi element paydo bo'lgan qator va ustunni aqliy ravishda kesib tashlang:

Xo'sh, birinchi qatorning uchinchi elementi. Originallik yo'q:

7) Belgilar matritsasidan tegishli belgini yozamiz:

8) Uchinchi elementni yozing:

9) Uchinchi elementni o'z ichiga olgan qator va ustunni aqliy ravishda kesib tashlang:

Qolgan to'rtta raqamni kichik determinantga yozamiz.

Qolgan harakatlar hech qanday qiyinchilik tug'dirmaydi, chunki biz allaqachon ikkitadan ikkita aniqlovchilarni qanday hisoblashni bilamiz. BELGILARDA ADALGANMANG!

Xuddi shunday, determinant istalgan satr yoki ustunga kengaytirilishi mumkin. Tabiiyki, oltita holatda ham javob bir xil.

To'rtdan to'rtta determinantni bir xil algoritm yordamida hisoblash mumkin.
Bunday holda, bizning belgilar matritsasi ortadi:

Quyidagi misolda men determinantni kengaytirdim to'rtinchi ustunga muvofiq:

Bu qanday sodir bo'ldi, buni o'zingiz aniqlashga harakat qiling. Batafsil ma'lumot keyinroq keladi. Agar kimdir determinantni oxirigacha yechmoqchi bo'lsa, to'g'ri javob: 18. Amaliyot uchun aniqlovchini boshqa ustun yoki boshqa qator bilan yechish yaxshiroqdir.

Mashq qilish, ochish, hisob-kitob qilish juda yaxshi va foydali. Lekin katta saralash uchun qancha vaqt sarflaysiz? Tezroq va ishonchliroq yo'l yo'qmi? Men sizga ikkinchi darsda determinantlarni hisoblashning samarali usullari bilan tanishishingizni taklif qilaman - Determinantning xususiyatlari. Determinantning tartibini qisqartirish.

DIQQATLI BO'LING!

Determinantlarni hisoblash n- tartib:

Determinant tushunchasi n-chi tartib

Determinantlar bo'yicha ushbu maqoladan foydalanib, siz quyidagi kabi muammolarni qanday hal qilishni o'rganasiz:

Tenglamani yeching:

va o'qituvchilar yaxshi ko'radigan ko'plab boshqalar.

Matritsaning determinanti yoki oddiygina determinant chiziqli tenglamalar tizimini echishda muhim rol o'ynaydi. Umuman olganda, determinantlar shu maqsadda ixtiro qilingan. Ular ko'pincha "matritsaning determinanti" deb ham aytadilar, biz bu erda matritsalarni ham eslatib o'tamiz. Matritsa o'zaro almashtirib bo'lmaydigan raqamlardan tuzilgan to'rtburchaklar jadval. Kvadrat matritsa - bu qatorlar va ustunlar soni bir xil bo'lgan jadval. Faqat kvadrat matritsa determinantga ega bo'lishi mumkin.

Determinantlarni yozish mantiqini quyidagi sxema yordamida tushunish oson. Sizga maktabdan tanish bo'lgan ikkita noma'lumli ikkita tenglama tizimini olaylik:

Determinantda noma'lumlar uchun koeffitsientlar ketma-ket yoziladi: birinchi qatorda - birinchi tenglamadan, ikkinchi qatorda - ikkinchi tenglamadan:

Masalan, tenglamalar sistemasi berilsa

u holda noma'lumlar koeffitsientlaridan quyidagi determinant hosil bo'ladi:

Shunday qilib, bizga tartiblangan raqamlardan iborat kvadrat jadval berilsin n chiziqlar (gorizontal qatorlar) va ichida n ustunlar (vertikal qatorlar). Ushbu raqamlardan foydalanib, biz quyida o'rganadigan ba'zi qoidalarga ko'ra, ular chaqirilgan raqamni topadilar aniqlovchi n--chi tartib va quyidagicha belgilansin:

(1)

Raqamlar chaqiriladi elementlar determinant (1) (birinchi indeks satr raqamini, ikkinchisi - element joylashgan chorrahada ustun raqamini bildiradi; i = 1, 2, ..., n; j= 1, 2, ..., n). Aniqlovchining tartibi uning satr va ustunlar sonidir.

Determinantning ikkala indeksi bir xil bo'lgan elementlarini bog'laydigan xayoliy to'g'ri chiziq, ya'ni. elementlar

chaqirdi asosiy diagonali, boshqa diagonal - tomoni.

Ikkinchi va uchinchi tartibli determinantlarni hisoblash

Keling, dastlabki uchta tartibning determinantlari qanday hisoblanganligini ko'rsatamiz.

Birinchi tartibli determinant elementning o'zi, ya'ni.

Ikkinchi tartibli determinant quyidagicha olingan sondir:

, (2)

Asosiy va ikkinchi darajali diagonallarda joylashgan elementlarning mahsuloti.

Tenglik (2) asosiy diagonal elementlarining mahsuloti o'z belgisi bilan, ikkinchi darajali diagonal elementlarining ko'paytmasi esa qarama-qarshi belgi bilan olinganligini ko'rsatadi. .

1-misol. Ikkinchi tartibli determinantlarni hisoblang:

Yechim. Formula (2) yordamida biz quyidagilarni topamiz:

Uchinchi tartibli determinant quyidagicha olingan sondir:

(3)

Ushbu formulani eslab qolish qiyin. Biroq, deb ataladigan oddiy qoida mavjud uchburchak qoidasi , bu ifodani takrorlashni osonlashtiradi (3). Determinantning elementlarini nuqtalar bilan belgilab, ularning determinant elementlarining mahsulotini beradiganlarini to'g'ri chiziq segmentlari bilan bog'laymiz (1-rasm).

Formula (3) shuni ko'rsatadiki, asosiy diagonal elementlarining ko'paytmalari, shuningdek, asoslari unga parallel bo'lgan ikkita uchburchakning cho'qqilarida joylashgan elementlar, ularning belgilari bilan olinadi; qarama-qarshi bo'lganlar bilan - yon diagonalning elementlari, shuningdek unga parallel bo'lgan ikkita uchburchakning tepalarida joylashgan elementlarning mahsuloti .

1-rasmda uchburchaklarning asosiy diagonali va mos keladigan asoslari va ikkilamchi diagonali va mos keladigan asoslari qizil rang bilan ajratilgan.

Determinantlarni hisoblashda, xuddi o'rta maktabda bo'lgani kabi, minus belgisi bo'lgan raqamning minus belgisi bo'lgan songa ko'paytirilishi natijasida ortiqcha belgisi bo'lgan raqam va ortiqcha belgisi bo'lgan raqam bir ga ko'paytirilishini yodda tutish juda muhimdir. minus belgisi bo'lgan raqam minus belgisi bo'lgan raqamni beradi.

2-misol. Uchinchi tartibli determinantni hisoblang:

Yechim. Uchburchak qoidasidan foydalanib, biz olamiz

Determinantlarni hisoblash n-chi tartib

Aniqlovchini satr yoki ustun bo'yicha kengaytirish

Determinantni hisoblash uchun n-chi tartib uchun siz quyidagi teoremani bilishingiz va ishlatishingiz kerak.

Laplas teoremasi. Determinant har qanday qatorning elementlari va ularning algebraik to'ldiruvchilari mahsuloti yig'indisiga teng, ya'ni.

Ta'rif. Agar determinantda bo'lsa n buyurtma - o'zboshimchalik bilan tanlang p chiziqlar va p ustunlar ( p < n), keyin bu satr va ustunlar kesishmasida joylashgan elementlar tartib matritsasini hosil qiladi.

Ushbu matritsaning determinanti deyiladi kichik asl determinant. Masalan, determinantni ko'rib chiqing:

Juft sonli satr va ustunlardan matritsa tuzamiz:

Aniqlovchi

chaqirdi kichik aniqlovchi Biz ikkinchi darajali kichikni oldik. Bundan ko'rinib turibdiki, biz birinchi, ikkinchi va uchinchi darajali turli xil voyaga etmaganlarni qurishimiz mumkin.

Agar biror elementni olib, u turgan determinantdagi satr va ustunni kesib tashlasak, minor elementi deb ataladigan minorni olamiz, uni quyidagicha belgilaymiz:

Agar minor ga ko'paytirilsa, bu erda 3 + 2 - kesishmasida element mavjud bo'lgan satr va ustun raqamlarining yig'indisi, u holda hosil bo'lgan mahsulot deyiladi. algebraik to‘ldiruvchi element va bilan belgilanadi

Umuman olganda, biz elementning minorini va algebraik to'ldiruvchini belgilaymiz,

(4)

Masalan, elementlarning algebraik to'ldiruvchilarini va uchinchi tartibli determinantni hisoblaymiz:

Formuladan foydalanib (4) olamiz

Aniqlovchini parchalashda ko'pincha aniqlovchining quyidagi xossasi qo'llaniladi n- tartib:

Agar satr yoki ustunning elementlariga boshqa satr yoki ustunning mos keladigan elementlarining ko'paytmasini doimiy koeffitsient bilan qo'shsangiz, determinantning qiymati o'zgarmaydi.

4-misol.

Birinchidan, birinchi va uchinchi qatorlardan to'rtinchi qatorning elementlarini olib tashlang, keyin bizda bo'ladi

Olingan determinantning to'rtinchi ustuni uchta elementni o'z ichiga oladi - nol. Shuning uchun, ushbu determinantni to'rtinchi ustun elementlariga kengaytirish foydaliroqdir, chunki dastlabki uchta mahsulot nolga teng bo'ladi. Shunung uchun

yordamida yechimni tekshirishingiz mumkin onlayn determinant kalkulyatori .

Va quyidagi misolda har qanday (bu holda, to'rtinchi) tartibli determinantning hisobini ikkinchi tartibli determinantning hisobiga qisqartirish mumkinligi ko'rsatilgan.

5-misol. Determinantni hisoblang:

Uchinchi qatordan birinchi qatorning elementlarini ayirib, birinchi qatorning elementlarini to'rtinchi qatorning elementlariga qo'shamiz, shunda bizda bo'ladi.

Birinchi ustunda birinchisidan tashqari barcha elementlar nolga teng. Ya'ni, determinant allaqachon birinchi ustun bo'ylab kengaytirilishi mumkin. Ammo biz uchinchi darajali determinantni hisoblashni xohlamaymiz. Shuning uchun biz yana bir nechta o'zgarishlarni amalga oshiramiz: uchinchi qatorning elementlariga biz ikkinchi qatorning elementlarini 2 ga ko'paytiramiz va to'rtinchi qatorning elementlaridan ikkinchi qatorning elementlarini ayiramiz. Natijada, algebraik to'ldiruvchi bo'lgan determinantning o'zi birinchi ustun bo'ylab kengaytirilishi mumkin va biz faqat ikkinchi tartibli determinantni hisoblashimiz kerak va belgilarda adashmaslik kerak:

Determinantni uchburchak shaklga keltirish

Diagonallardan birining bir tomonida joylashgan barcha elementlar nolga teng bo'lgan determinantga uchburchak deyiladi. Satrlar yoki ustunlar tartibini teskari o'zgartirish orqali ikkilamchi diagonalning holati asosiy diagonalning holatiga qisqartiriladi. Bu determinant asosiy diagonal elementlarining mahsulotiga teng.

Uchburchak shaklga keltirish uchun determinantning bir xil xususiyatidan foydalaniladi n- oldingi bandda biz qo'llagan tartib: agar satr yoki ustun elementlariga boshqa satr yoki ustunning mos keladigan elementlarining ko'paytmasi doimiy koeffitsient bilan qo'shilsa, determinantning qiymati o'zgarmaydi.

yordamida yechimni tekshirishingiz mumkin onlayn determinant kalkulyatori .

Determinantning xossalari n-chi tartib

Oldingi ikkita paragrafda biz determinantning xususiyatlaridan birini ishlatgan edik n-chi tartib. Ayrim hollarda determinantni hisoblashni soddalashtirish uchun determinantning boshqa muhim xususiyatlaridan foydalanish mumkin. Misol uchun, determinantni ikkita determinantning yig'indisiga qisqartirish mumkin, ulardan biri yoki ikkalasi ham biron bir satr yoki ustunda qulay tarzda kengaytirilishi mumkin. Bunday soddalashtirish holatlari juda ko'p va aniqlovchining u yoki bu xususiyatidan foydalanish masalasi alohida hal qilinishi kerak.

Ko'pincha universitetlarda biz oliy matematikadan zarur bo'lgan muammolarga duch kelamiz matritsaning determinantini hisoblang. Aytgancha, determinant faqat kvadrat matritsalarda bo'lishi mumkin. Quyida biz asosiy ta'riflarni, determinant qanday xususiyatlarga ega ekanligini va uni qanday to'g'ri hisoblashni ko'rib chiqamiz.Shuningdek, misollar yordamida batafsil yechimni ko'rsatamiz.

Matritsaning aniqlovchisi nima: ta'rifdan foydalanib determinantni hisoblash

Matritsa determinanti

Ikkinchi tartib raqamdir.

Matritsaning determinanti - (determinantlarning lotincha nomining qisqartmasi) yoki .

Agar:, keyin chiqadi

Yana bir nechta yordamchi ta'riflarni eslaylik:

Ta'rif

Elementlardan tashkil topgan tartiblangan sonlar to‘plami tartib o‘rnini almashtirish deyiladi.

Elementlarni o'z ichiga olgan to'plam uchun faktorial (n) mavjud bo'lib, u doimo undov belgisi bilan belgilanadi: . O'zgartirishlar bir-biridan faqat paydo bo'lish tartibi bilan farqlanadi. Buni aniqroq qilish uchun misol keltiramiz:

Uchta elementdan iborat to'plamni ko'rib chiqing (3, 6, 7). Jami 6 ta almashtirish mavjud, chunki .:

Ta'rif

Tartibni almashtirishdagi inversiya tartiblangan raqamlar to'plamidir (uni bijeksiya deb ham ataladi), bunda ulardan ikkitasi o'ziga xos tartibsizlikni hosil qiladi. Bu berilgan almashtirishdagi katta raqam kichikroq raqamning chap tomonida joylashganida.

Yuqorida biz almashtirishning inversiyasi misolini ko'rib chiqdik, bu erda raqamlar mavjud edi. Shunday qilib, keling, ikkinchi qatorni olaylik, bu erda bu raqamlarga ko'ra, a , chunki ikkinchi element uchinchi elementdan kattaroqdir. Taqqoslash uchun raqamlar joylashgan oltinchi qatorni olaylik: . Bu yerda uchta juftlik mavjud: , va , chunki title=" QuickLaTeX.com tomonidan taqdim etilgan)" height="13" width="42" style="vertical-align: 0px;">; , так как title="QuickLaTeX.com tomonidan taqdim etilgan" height="13" width="42" style="vertical-align: 0px;">; , – title="QuickLaTeX.com tomonidan taqdim etilgan" height="12" width="43" style="vertical-align: 0px;">.!}

Biz inversiyaning o'zini o'rganmaymiz, lekin mavzuni keyingi ko'rib chiqishda almashtirishlar biz uchun juda foydali bo'ladi.

Ta'rif

x matritsaning aniqlovchisi - son:

1 dan cheksiz songacha bo'lgan sonlarning almashtirilishi va almashtirishdagi inversiyalar soni. Shunday qilib, determinant "aniqlovchining shartlari" deb ataladigan atamalarni o'z ichiga oladi.

Siz ikkinchi, uchinchi va hatto to'rtinchi tartibli matritsaning determinantini hisoblashingiz mumkin. Shuningdek, aytib o'tish joiz:

Ta'rif

Matritsaning determinanti teng bo'lgan sondir

Ushbu formulani tushunish uchun uni batafsilroq tasvirlab beraylik. Kvadrat matritsa x ning determinanti - bu hadlarni o'z ichiga olgan yig'indi va har bir atama ma'lum miqdordagi matritsa elementlarining mahsulotidir. Bundan tashqari, har bir mahsulotda matritsaning har bir satri va ustunidan element mavjud.

Agar mahsulotdagi matritsa elementlari tartibda bo'lsa (satr raqami bo'yicha) va ko'plab ustun raqamlarini almashtirishdagi inversiyalar soni toq bo'lsa, u ma'lum bir muddatdan oldin paydo bo'lishi mumkin.

Yuqorida aytib o'tilgan ediki, matritsaning aniqlovchisi yoki bilan belgilanadi, ya'ni determinant ko'pincha determinant deb ataladi.

Shunday qilib, formulaga qaytaylik:

Formuladan ko'rinib turibdiki, birinchi tartibli matritsaning determinanti xuddi shu matritsaning elementi.

Ikkinchi tartibli matritsaning determinantini hisoblash

Ko'pincha amaliyotda matritsaning determinanti ikkinchi, uchinchi va kamroq to'rtinchi tartibli usullar yordamida hal qilinadi. Keling, ikkinchi tartibli matritsaning determinanti qanday hisoblanishini ko'rib chiqaylik:

Ikkinchi tartibli matritsada faktorialning . Formulani qo'llashdan oldin

Biz qanday ma'lumotlarni olishimizni aniqlashimiz kerak:

2. to'plamlarning almashtirishlari: va ;

3. almashtirishdagi inversiyalar soni : va , chunki title=" QuickLaTeX.com tomonidan ko'rsatilgan)" height="13" width="42" style="vertical-align: -1px;">;!}

4. tegishli ishlar: va.

Ma'lum bo'lishicha:

Yuqoridagilarga asoslanib, biz ikkinchi tartibli kvadrat matritsaning determinantini, ya'ni x ni hisoblash formulasini olamiz:

Ikkinchi tartibli kvadrat matritsaning determinantini hisoblashning aniq misolini ko'rib chiqaylik:

Misol

Vazifa

x matritsasining determinantini hisoblang:

Yechim

Shunday qilib, biz , , , ni olamiz.

Yechish uchun siz ilgari muhokama qilingan formuladan foydalanishingiz kerak:

Biz misoldagi raqamlarni almashtiramiz va topamiz:

Javob

Ikkinchi tartibli matritsa determinanti =.

Uchinchi tartibli matritsaning determinantini hisoblash: formula yordamida misol va yechim

Ta'rif

Uchinchi tartibli matritsaning determinanti kvadrat jadvalda joylashgan to'qqizta berilgan sondan olingan raqam,

Uchinchi tartib aniqlovchi ikkinchi tartibli aniqlovchi bilan deyarli bir xil tarzda topiladi. Farqi faqat formulada. Shuning uchun, agar siz formulani yaxshi tushunsangiz, unda yechim bilan bog'liq muammolar bo'lmaydi.

Uchinchi tartibli kvadrat matritsani ko'rib chiqing *:

Ushbu matritsaga asoslanib, biz shunga mos ravishda faktorial = ekanligini tushunamiz, ya'ni umumiy almashtirishlar

Formulani to'g'ri qo'llash uchun siz ma'lumotlarni topishingiz kerak:

Shunday qilib, to'plamning umumiy almashtirishlari:

O'zgartirishdagi inversiyalar soni , va mos keladigan mahsulotlar = ;

Permutatsiyadagi inversiyalar soni title="QuickLaTeX.com tomonidan ko'rsatilgan" height="18" width="65" style="vertical-align: -4px;">, соответствующие произведения = ;!}

Permutatsiyadagi inversiyalar title=" QuickLaTeX.com tomonidan ko'rsatilgan" height="18" width="65" style="vertical-align: -4px;"> ;!}

. ; o'zgartirish sarlavhasi = " QuickLaTeX.com tomonidan ko'rsatilgan" height="18" width="118" style="vertical-align: -4px;">, соответствующие произведение = !}

. ; o'zgartirish sarlavhasi = " QuickLaTeX.com tomonidan ko'rsatilgan" height="18" width="171" style="vertical-align: -4px;">, соответствующие произведение = .!}

Endi biz olamiz:

Shunday qilib, bizda x tartibli matritsaning determinantini hisoblash uchun formula mavjud:

Uchburchak qoidasi yordamida uchinchi tartibli matritsani topish (Sarrus qoidasi)

Yuqorida aytib o'tilganidek, 3-tartibli determinantning elementlari uchta qator va uchta ustunda joylashgan. Agar siz umumiy elementning belgilanishini kiritsangiz, unda birinchi element satr raqamini, indekslardan ikkinchi element esa ustun raqamini bildiradi. Aniqlovchining asosiy (elementlari) va ikkilamchi (elementlari) diagonallari mavjud. O'ng tarafdagi shartlar aniqlovchining hadlari deyiladi).

Ko'rinib turibdiki, determinantning har bir a'zosi diagrammada har bir satr va har bir ustunda faqat bitta elementdan iborat.

Determinantni diagramma shaklida tasvirlangan to'rtburchaklar qoidasi yordamida hisoblashingiz mumkin. Asosiy diagonalning elementlaridan determinantning shartlari qizil rangda, shuningdek, asosiy diagonalga bir tomoni parallel bo'lgan uchburchaklar cho'qqisida joylashgan elementlardan atamalar (chap diagramma) belgisi bilan ajratilgan. .

Yon diagonal elementlaridan, shuningdek, yon diagonalga parallel tomonlari bo'lgan uchburchaklar cho'qqilarida joylashgan elementlardan (o'ng diagramma) ko'k o'qli atamalar belgi bilan olinadi.

Quyidagi misoldan foydalanib, uchinchi tartibli kvadrat matritsaning determinantini hisoblashni o'rganamiz.

Misol

Vazifa

Uchinchi tartibli matritsaning determinantini hisoblang:

Yechim

Ushbu misolda:

Yuqorida muhokama qilingan formula yoki sxema yordamida determinantni hisoblaymiz:

Javob

Uchinchi tartibli matritsaning aniqlovchisi =

Uchinchi tartibli matritsa determinantlarining asosiy xossalari

Oldingi ta'riflar va formulalarga asoslanib, asosiysini ko'rib chiqaylik matritsa determinantining xossalari.

1. Tegishli satr va ustunlarni almashtirishda determinantning o'lchami o'zgarmaydi (bunday almashtirish transpozitsiya deb ataladi).

Misol yordamida biz matritsaning determinanti transpozitsiya qilingan matritsaning determinantiga teng ekanligiga ishonch hosil qilamiz:

Determinantni hisoblash formulasini eslaylik:

Matritsani ko'chiring:

O'tkazilgan matritsaning determinantini hisoblaymiz:

Biz ko'chirilgan matritsaning determinanti to'g'ri echimni ko'rsatadigan asl matritsaga teng ekanligini tasdiqladik.

2. Determinantning har qanday ikkita ustuni yoki ikkita satri almashtirilsa, uning belgisi teskari tomonga o'zgaradi.

Keling, bir misolni ko'rib chiqaylik:

Ikkita uchinchi tartibli matritsalar (x) berilgan:

Bu matritsalarning determinantlari qarama-qarshi ekanligini ko'rsatish kerak.

Yechim

Matritsadagi va matritsadagi qatorlar o'zgargan (birinchidan uchinchi, birinchidan uchinchisiga). Ikkinchi xususiyatga ko'ra, ikkita matritsaning determinantlari bir-biridan belgisi bo'yicha farq qilishi kerak. Ya'ni, bitta matritsa ijobiy, ikkinchisi esa salbiy belgiga ega. Determinantni hisoblash uchun formuladan foydalanib, ushbu xususiyatni tekshiramiz.

Mulk haqiqatdir, chunki.

3. Determinant ikki satrda (ustunlarda) bir xil mos elementlarga ega bo'lsa, nolga teng bo'ladi. Determinant birinchi va ikkinchi ustunlarning bir xil elementlariga ega bo'lsin:

Bir xil ustunlarni almashtirib, biz 2-xususiyatga ko'ra, yangi determinantni olamiz: = . Boshqa tomondan, yangi determinant asl bilan mos keladi, chunki elementlarning javoblari bir xil, ya'ni = . Bu tengliklardan biz olamiz: = .

4. Agar bitta satr (ustun) ning barcha elementlari nolga teng bo'lsa, determinant nolga teng. Bu gap shundan kelib chiqadiki, formula (1) bo'yicha determinantning har bir a'zosi bitta va har bir satrdan (ustun) faqat bitta elementga ega bo'lib, u faqat nolga ega.

Keling, bir misolni ko'rib chiqaylik:

Keling, matritsaning determinanti nolga teng ekanligini ko'rsatamiz:

Bizning matritsamiz ikkita bir xil ustunga ega (ikkinchi va uchinchi), shuning uchun ushbu xususiyatga asoslanib, determinant nolga teng bo'lishi kerak. Keling, tekshiramiz:

Darhaqiqat, ikkita bir xil ustunli matritsaning determinanti nolga teng.

5. Birinchi qator (ustun) elementlarining umumiy omili determinant belgisidan chiqarilishi mumkin:

6. Agar determinantning bir satri yoki bitta ustunining elementlari ikkinchi qatorning (ustunning) mos keladigan elementlariga proporsional bo'lsa, unda bunday determinant nolga teng bo'ladi.

Haqiqatan ham, 5-xususiyatdan keyin mutanosiblik koeffitsientini aniqlovchi belgisidan chiqarish mumkin, keyin esa 3-xususiyatdan foydalanish mumkin.

7. Agar determinant satrlari (ustunlari) elementlarining har biri ikkita hadning yig'indisi bo'lsa, u holda bu aniqlovchi mos keladigan aniqlovchilarning yig'indisi sifatida taqdim etilishi mumkin:

Tekshirish uchun (1) tenglikning chap tomonida joylashgan aniqlovchiga muvofiq kengaytirilgan shaklda yozish kifoya, so'ngra va elementlarini o'z ichiga olgan atamalarni alohida guruhlash kifoya qiladi.Olingan atamalar guruhining har biri mos ravishda bo'ladi. , tenglikning o'ng tomonidagi birinchi va ikkinchi aniqlovchi.

8. Agar bitta satr yoki ustun elementiga ikkinchi qatorning (ustun) mos keladigan elementlari bir xil raqamga ko'paytirilsa, ta'rif qiymatlari o'zgarmaydi:

Bu tenglik 6 va 7 xossalar asosida olinadi.

9. Matritsaning aniqlovchisi, , har qanday satr yoki ustun elementlari va ularning algebraik to'ldiruvchilari ko'paytmalari yig'indisiga teng.

Bu erda matritsa elementining algebraik to'ldiruvchisi orqali. Bu xususiyatdan foydalanib, siz nafaqat uchinchi tartibli matritsalarni, balki yuqori tartibli (x yoki x) matritsalarni ham hisoblashingiz mumkin.Boshqacha qilib aytganda, bu har qanday tartibli matritsaning determinantini hisoblash uchun zarur bo'lgan takrorlanuvchi formuladir. . Uni eslab qoling, chunki u ko'pincha amalda qo'llaniladi.

Aytish joizki, to'qqizinchi xususiyatdan foydalanib, nafaqat to'rtinchi tartibli, balki yuqori darajali matritsalarning determinantlarini ham hisoblash mumkin. Biroq, bu holda siz juda ko'p hisoblash operatsiyalarini bajarishingiz va ehtiyot bo'lishingiz kerak, chunki belgilardagi eng kichik xato noto'g'ri qarorga olib keladi. Gauss usuli yordamida yuqori tartibli matritsalarni yechish eng qulaydir va bu haqda keyinroq gaplashamiz.

10. Bir xil tartibli matritsalar ko'paytmasining aniqlovchisi ularning aniqlovchilarining ko'paytmasiga teng.

Keling, bir misolni ko'rib chiqaylik:

Misol

Vazifa

Ikki matritsaning determinanti va ularning determinantlarining mahsulotiga teng ekanligiga ishonch hosil qiling. Ikki matritsa berilgan:

Yechim

Birinchidan, ikkita matritsa va determinantlarining ko'paytmasini topamiz.

Endi ikkala matritsani ko'paytiramiz va shunday qilib determinantni hisoblaymiz:

Javob

Biz bunga ishonch hosil qildik