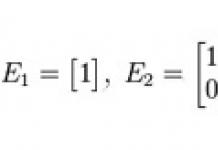Нехай є квадратна матриця n-го порядку

Матриця А-1 називається зворотною матрицеюстосовно матриці А, якщо А*А -1 = Е, де Е — одинична матриця n-го порядку.

Одинична матриця- Така квадратна матриця, у якої всі елементи по головній діагоналі, що проходить від лівого верхнього кута до правого нижнього кута, - одиниці, а інші - нулі, наприклад:

зворотна матрицяможе існувати тільки для квадратних матрицьтобто. для тих матриць, у яких число рядків та стовпців збігаються.

Теорема умови існування зворотної матриці

Для того, щоб матриця мала зворотну матрицю, необхідно і достатньо, щоб вона була невиродженою.

Матриця А = (А1, А2, ... Аn) називається невиродженоюякщо вектори-стовпці є лінійно незалежними. Число лінійно незалежних векторів-стовпців матриці називається рангом матриці. Тому можна сказати, що для того, щоб існувала обернена матриця, необхідно і достатньо, щоб ранг матриці дорівнював її розмірності, тобто. r = n.

Алгоритм знаходження зворотної матриці

1. Записати до таблиці на вирішення систем рівнянь методом Гаусса матрицю А і праворуч (на місце правих частин рівнянь) приписати до неї матрицю Е.
2. Використовуючи перетворення Жордана, привести матрицю до матриці, що складається з одиничних стовпців; при цьому необхідно одночасно перетворити матрицю Е.
3. Якщо необхідно, то переставити рядки (рівняння) останньої таблиці так, щоб під матрицею вихідної таблиці А вийшла одинична матриця Е.
4. Записати зворотну матрицю А-1, яка знаходиться в останній таблиці під матрицею Е вихідної таблиці.

Приклад 1

Для матриці А знайти зворотну матрицю А-1

Рішення: Записуємо матрицю А і праворуч приписуємо одиничну матрицю Е. Використовуючи перетворення Жордана, наводимо матрицю А до одиничної матриці Е. Обчислення наведено у таблиці 31.1.

Перевіримо правильність обчислень множенням вихідної матриці А та зворотної матриці А-1.

В результаті множення матриць вийшла поодинока матриця. Отже, обчислення зроблено правильно.

Відповідь:

Розв'язання матричних рівнянь

Матричні рівняння можуть мати вигляд:

АХ = В, ХА = В, АХВ = С,

де А, В, С - матриці, що задаються, Х - шукана матриця.

Матричні рівняння вирішуються з допомогою множення рівняння зворотні матриці.

Наприклад, щоб знайти матрицю з рівняння необхідно помножити це рівняння на ліворуч.

Отже, щоб знайти рішення рівняння потрібно знайти зворотну матрицю і помножити її на матрицю , що стоять у правій частині рівняння.

Аналогічно вирішуються інші рівняння.

Приклад 2

Розв'язати рівняння АХ = В, якщо

Рішення: Оскільки зворотна матриця дорівнює (див. приклад 1)

Матричний метод в економічному аналізі

Поряд з іншими знаходять застосування також матричні методи. Ці методи базуються на лінійній та векторно-матричній алгебрі. Такі методи застосовуються з метою аналізу складних та багатовимірних економічних явищ. Найчастіше ці методи використовуються за необхідності порівняльної оцінки функціонування організацій та його структурних підрозділів.

У процесі застосування матричних методів аналізу можна виділити кілька етапів.

На першому етапіздійснюється формування системи економічних показників і на її основі складається матриця вихідних даних , яка є таблицею, в якій за її окремими рядками показуються номери систем (i = 1,2,...,,n), а за вертикальними графами - номери показників (j = 1,2,....,m).

На другому етапіпо кожній вертикальній графі виявляється найбільше з існуючих значень показників, яке приймається за одиницю.

Після цього всі суми, відображені в даній графі поділяють найбільше значення і формується матриця стандартизованих коефіцієнтів .

На третьому етапівсі складові матриці зводять у квадрат. Якщо вони мають різну значимість, то кожному показнику матриці надається певний ваговий коефіцієнт k. Розмір останнього визначається експертним шляхом.

На останньому, четвертому етапізнайдені величини рейтингових оцінок R jгрупуються у порядку їх збільшення чи зменшення.

Викладені матричні методи слід використовувати, наприклад, для порівняльного аналізу різних інвестиційних проектів, а також для оцінки інших економічних показників діяльності організацій.

Для будь-якої невиродженої матриці А існує і єдина матриця A -1 така, що

A*A -1 =A -1 *A = E,

де E — одинична матриця тих самих порядків, як і А. Матриця A -1 називається зворотної до матриці A.

Якщо хтось забув, в одиничній матриці, крім діагоналі, заповненої одиницями, всі інші позиції заповнені нулями, приклад одиничної матриці:

Знаходження зворотної матриці методом приєднаної матриці

Зворотна матриця визначається формулою:

де A ij - елементів a ij.

Тобто. для обчислення зворотної матриці потрібно обчислити визначник цієї матриці. Потім знайти додатки алгебри для всіх її елементів і скласти з них нову матрицю. Далі потрібно транспортувати цю матрицю. І кожен елемент нової матриці розділити на визначник вихідної матриці.

Розглянемо кілька прикладів.

Знайти A-1 для матриці

Розв'язання. Знайдемо A -1 методом приєднаної матриці. Маємо det A = 2. Знайдемо алгебраїчні доповнення елементів матриці A. У цьому випадку алгебраїчними доповненнями елементів матриці будуть відповідні елементи самої матриці, взяті зі знаком відповідно до формули

Маємо A 11 = 3, A 12 = -4, A 21 = -1, A 22 = 2. Утворимо приєднану матрицю

Транспортуємо матрицю A*:

Знаходимо зворотну матрицю за формулою:

Отримуємо:

Методом приєднаної матриці знайти A-1, якщо

Розв'язання. Перш за все обчислюємо визначтеся даної матриці, щоб переконатися в існуванні зворотної матриці. Маємо

Тут ми додали до елементів другого рядка елементи третього рядка, помножені попередньо (-1), а потім розкрили визначник по другому рядку. Оскільки визначитеся даної матриці відмінний від нуля, то зворотна до неї матриця існує. Для побудови приєднаної матриці знаходимо додатки алгебри елементів даної матриці. Маємо

Відповідно до формули

транспортуємо матрицю A*:

Тоді за формулою

Знаходження зворотної матриці методом елементарних перетворень

Крім методу знаходження зворотної матриці, що з формули (метод приєднаної матриці), існує метод знаходження зворотної матриці, званий методом елементарних перетворень.

Елементарні перетворення матриці

Елементарними перетвореннями матриці називаються такі перетворення:

1) перестановка рядків (стовпців);

2) множення рядка (стовпця) на число, відмінне від нуля;

3) додавання до елементів рядка (стовпця) відповідних елементів іншого рядка (стовпця), попередньо помножених на деяке число.

Для знаходження матриці A -1 побудуємо прямокутну матрицю В = (А|Е) порядків (n; 2n), приписуючи до матриці А справа одиничну матрицю Е через роздільну межу:

Розглянемо приклад.

Методом елементарних перетворень знайти A -1 якщо

Рішення. Утворимо матрицю B:

Позначимо рядки матриці B через 1 , 2 , 3 . Зробимо над рядками матриці B наступні перетворення.

Ця тема є однією з найненависніших серед студентів. Гірше, мабуть, лише визначники.

Фішка в тому, що саме поняття зворотного елемента (і я зараз не лише про матриці) відсилає нас до операції множення. Навіть у шкільній програмі множення вважається складною операцією, а множення матриць — взагалі окрема тема, якій у мене присвячений цілий параграф і відеоурок.

Сьогодні ми не будемо вдаватися до подробиць матричних обчислень. Просто згадаємо: як позначаються матриці, як вони множаться і що з цього випливає.

Повторення: множення матриць

Насамперед домовимося про позначення. Матрицею $A$ розміру $\left[ m\times n \right]$ називається просто таблиця з чисел, в якій рівно $m$ рядків і $n$ стовпців:

\=\underbrace(\left[ \begin(matrix) ((a)_(11)) & ((a)_(12)) & ... & ((a)_(1n)) \\ (( a)_(21)) & ((a)_(22)) & ... & ((a)_(2n)) \\ ... & ... & ... & ... \\ ((a)_(m1)) & ((a)_(m2)) & ... & ((a)_(mn)) \\\end(matrix) \right])_(n)\]

Щоб випадково не переплутати рядки та стовпці місцями (повірте, на іспиті можна і одиницю з двійкою переплутати — що вже казати про якісь там рядки), просто погляньте на картинку:

Визначення індексів для клітин матриці

Що відбувається? Якщо розмістити стандартну систему координат $OXY$ у лівому верхньому кутку і направити осі так, щоб вони охоплювали всю матрицю, то кожній клітині цієї матриці можна однозначно зіставити координати $\left(x;y \right)$ - це і буде номер рядка і номер стовпця.

Чому система координат розміщена саме у лівому верхньому кутку? Бо саме звідти ми починаємо читати будь-які тексти. Це просто запам'ятати.

А чому вісь $x$ спрямована саме вниз, а не праворуч? Знову все просто: візьміть стандартну систему координат (вісь $x$ йде вправо, вісь $y$ вгору) і поверніть її так, щоб вона охоплювала матрицю. Це поворот на 90 градусів за годинниковою стрілкою – його результат ми й бачимо на картинці.

Загалом, як визначити індекси у елементів матриці, ми розібралися. Тепер розберемося з множенням.

Визначення. Матриці $A=\left[ m\times n \right]$ і $B=\left[ n\times k \right]$, коли кількість стовпців у першій збігається з кількістю рядків у другій, називаються узгодженими.

Саме у такому порядку. Можна сумніватися і сказати, мовляв, матриці $A$ і $B$ утворюють впорядковану пару $\left(A;B \right)$: якщо вони узгоджені в такому порядку, то необов'язково, що $B$ і $A$, тобто. пара $ \ left (B; A \ right) $ - теж узгоджена.

Помножувати можна лише узгоджені матриці.

Визначення. Твір узгоджених матриць $A=\left[m\times n\right]$ і $B=\left[n\times k \right]$ - це нова матриця $C=\left[m\times k \right]$ елементи якої $((c)_(ij))$ вважаються за формулою:

\[((c)_(ij))=\sum\limits_(k=1)^(n)(((a)_(ik)))\cdot ((b)_(kj))\]

Іншими словами: щоб отримати елемент $((c)_(ij))$ матриці $C=A\cdot B$, потрібно взяти $i$-рядок першої матриці, $j$-й стовпець другої матриці, а потім попарно перемножити елементи з цього рядка та стовпця. Результати скласти.

Так, ось таке суворе визначення. З нього відразу випливає кілька фактів:

1. Множення матриць, взагалі кажучи, некомутативно: $ A \ cdot B \ ne B \ cdot A $;
2. Однак множення асоціативно: $ \ left (A cdot B \ right) \ cdot C = A \ cdot \ left (B \ cdot C \ right) $;
3. І навіть дистрибутивно: $ \ left (A + B \ right) \ cdot C = A cdot C + B cdot C $;
4. І ще раз дистрибутивно: $ A \ cdot \ left (B + C \ right) = A \ cdot B + A \ cdot C $.

Дистрибутивність множення довелося окремо описувати для лівого та правого множника-суми якраз через некомутативність операції множення.

Якщо все ж таки виходить так, що $A cdot B = B cdot A $, такі матриці називаються перестановочними.

Серед усіх матриць, які там на щось множаться, є особливі ті, які при множенні на будь-яку матрицю $A$ знову дають $A$:

Визначення. Матриця $E$ називається одиничною, якщо $A\cdot E=A$ або $E\cdot A=A$. У випадку з квадратною матрицею $A$ можемо записати:

Поодинока матриця - частий гість під час вирішення матричних рівнянь. І взагалі найчастіший гість у світі матриць.:)

А ще через цю $E$ дехто вигадав всю ту дичину, яка буде написана далі.

Що таке зворотна матриця

Оскільки множення матриць - дуже трудомістка операція (доводиться перемножувати купу рядків і стовпців), то поняття зворотної матриці теж виявляється не найбільш очевидним. І потребує деяких пояснень.

Ключове визначення

Що ж, настав час пізнати істину.

Визначення. Матриця $B$ називається зворотною до матриці $A$ , якщо

Зворотна матриця позначається через $((A)^(-1))$ (не плутати зі ступенем!), тому визначення можна переписати так:

Здавалося б, все дуже просто і ясно. Але під час аналізу такого визначення відразу виникає кілька питань:

1. Чи завжди є зворотна матриця? І якщо не завжди, то як визначити: коли вона існує, а коли ні?
2. А хто сказав, що така матриця одно? Раптом для деякої вихідної матриці $A$ знайдеться ціла юрба зворотних?
3. Як виглядають усі ці «зворотні»? І як, власне, їх рахувати?

Щодо алгоритмів обчислення – про це ми поговоримо трохи згодом. Але на інші питання відповімо зараз. Оформимо їх у вигляді окремих тверджень-лем.

Основні властивості

Почнемо з того, як у принципі має виглядати матриця $A$, щоб для неї існувала $((A)^(-1))$. Зараз ми переконаємося в тому, що обидві ці матриці повинні бути квадратними, причому одного розміру: $ \ left [n \ times n \ right] $.

Лемма 1 . Дана матриця $A$ і обернена їй $((A)^(-1))$. Тоді обидві ці матриці квадратні, причому однакового порядку $ n $.

Доведення. Все просто. Нехай матриця $A=\left[m\times n \right]$, $((A)^(-1))=\left[ a\times b \right]$. Оскільки добуток $A\cdot ((A)^(-1))=E$ за визначенням існує, матриці $A$ і $((A)^(-1))$ узгоджені у вказаному порядку:

\[\begin(align) & \left[ m\times n \right]\cdot \left[ a\times b \right]=\left[ m\times b \right] \\ & n=a \end( align)\]

Це прямий наслідок алгоритму перемноження матриць: коефіцієнти $n$ і $a$ є «транзитними» і мають бути рівними.

Водночас визначено і зворотне множення: $((A)^(-1))\cdot A=E$, тому матриці $((A)^(-1))$ і $A$ також узгоджені у вказаному порядку:

\[\begin(align) & \left[ a\times b \right]\cdot \left[ m\times n \right]=\left[ a\times n \right] \\ & b=m \end( align)\]

Отже, без обмеження спільності можемо вважати, що $A=\left[ m\times n \right]$, $((A)^(-1))=\left[ n\times m \right]$. Однак згідно з визначенням $A\cdot ((A)^(-1))=((A)^(-1))\cdot A$, тому розміри матриць суворо збігаються:

\[\begin(align) & \left[ m\times n \right]=\left[ n\times m \right] \\ & m=n \end(align)\]

Ось і виходить, що всі три матриці - $ A $, $ ((A) ^ (-1)) $ і $ E $ - є квадратними розміром $ \ left [n \ times n \ right] $. Лемма доведена.

Що ж, уже непогано. Ми, що оборотними бувають лише квадратні матриці. Тепер переконаємося, що зворотна матриця завжди одна.

Лемма 2 . Дана матриця $A$ і обернена їй $((A)^(-1))$. Тоді ця зворотна матриця єдина.

Доведення. Підемо від протилежного: нехай матриця $A$ має хоча б два екземпляри зворотних —$B$ і $C$. Тоді, згідно з визначенням, вірні такі рівності:

\[\begin(align) & A\cdot B=B\cdot A=E; \ & A \ cdot C = C \ cdot A = E. \\ \end(align)\]

З леми 1 ми укладаємо, що всі чотири матриці - $ A $, $ B $, $ C $ і $ E $ - є квадратними однакового порядку: $ \ left [n \ times n \ right] $. Отже, визначено твір:

Оскільки множення матриць асоціативно (але не комутативно!), ми можемо записати:

\\\\\begin(align) & B\cdot A\cdot C=\left(B\cdot A \right)\cdot C=E\cdot C=C; \ \ & B \ cdot A \ cdot C = B \ cdot \ left (A \ cdot C \ right) = B \ cdot E = B; \ & B \ cdot A \ cdot C = C = B \ Rightarrow B = C. \\ \end(align)\]

Отримали єдино можливий варіант: два екземпляри зворотної матриці рівні. Лемма доведена.

Наведені міркування майже дослівно повторюють доказ єдиність зворотного елемента всім дійсних чисел $b\ne 0$. Єдине істотне доповнення - облік розмірності матриць.

Втім, ми досі нічого не знаємо про те, чи квадратна матриця є оборотною. Тут нам на допомогу приходить визначник це ключова характеристика для всіх квадратних матриць.

Лемма 3 . Дано матрицю $A$. Якщо зворотна до неї матриця $((A)^(-1))$ існує, то визначник вихідної матриці відмінний від нуля:

\[\left| A \right|\ne 0\]

Доведення. Ми вже знаємо, що $A$ і $((A)^(-1))$ — квадратні матриці розміру $\left[ n\times n \right]$. Отже, кожної з них можна обчислити визначник: $\left| A \right|$ і $\left| ((A)^(-1)) \right|$. Проте визначник твору дорівнює твору визначників:

\[\left| A\cdot B \right|=\left| A \right|\cdot \left| B \right|\Rightarrow \left| A\cdot ((A)^(-1)) \right|=\left| A \right|\cdot \left| ((A)^(-1)) \right|\]

Але згідно з визначенням $A\cdot ((A)^(-1))=E$, а визначник $E$ завжди дорівнює 1, тому

\[\begin(align) & A\cdot ((A)^(-1))=E; \\ & \left| A\cdot ((A)^(-1)) \right|=\left| E \right|; \\ & \left| A \right|\cdot \left| ((A)^(-1)) \right|=1. \\ \end(align)\]

Добуток двох чисел дорівнює одиниці тільки в тому випадку, коли кожне з цих чисел відмінно від нуля:

\[\left| A \right|\ne 0;\quad \left| ((A)^(-1)) \right|\ne 0.\]

Ось і виходить, що $ \ left | A \right|\ne 0$. Лемма доведена.

Насправді ця вимога є цілком логічною. Зараз ми розберемо алгоритм знаходження зворотної матриці - і стане зрозуміло, чому за нульового визначника ніякої зворотної матриці в принципі не може існувати.

Але для початку сформулюємо «допоміжне» визначення:

Визначення. Вироджена матриця - це квадратна матриця розміру $ \ left [n \ times n \ right] $, чий визначник дорівнює нулю.

Таким чином, ми можемо стверджувати, що будь-яка оборотна матриця є невиродженою.

Як знайти зворотну матрицю

Зараз розглянемо універсальний алгоритм знаходження зворотних матриць. Взагалі, існує два загальноприйняті алгоритми, і другий ми також сьогодні розглянемо.

Той, який буде розглянутий зараз, дуже ефективний для матриць розміру $ \ left [2 \ times 2 \ right] $ і - частково - розміру $ \ left [3 \ times 3 \ right] $. А ось починаючи з розміру $ \ left [4 \ times 4 \ right] $ його краще не застосовувати. Чому зараз самі все зрозумієте.

Алгебраїчні доповнення

Готуйтеся. Нині буде біль. Ні, не хвилюйтеся: до вас не йде красива медсестра у спідниці, панчохах з мереживом і не зробить укол у сідницю. Все куди прозаїчніше: до вас йдуть алгебраїчні доповнення та її Величність «Союзна Матриця».

Почнемо з головного. Нехай є квадратна матриця розміру $ A = \ left [n \ times n \ right] $, елементи якої іменуються $ ((a)_ (ij)) $. Тоді для кожного такого елемента можна визначити додаток алгебри:

Визначення. Алгебраїчне доповнення $((A)_(ij))$ до елемента $((a)_(ij))$, що стоїть у $i$-му рядку і $j$-му стовпці матриці $A=\left[ n \times n \right]$ - це конструкція виду

\[((A)_(ij))=((\left(-1 \right))^(i+j))\cdot M_(ij)^(*)\]

Де $M_(ij)^(*)$ — визначник матриці, отриманої з вихідної $A$ викреслюванням того самого $i$-го рядка і $j$-го стовпця.

Ще раз. Додаток алгебри до елемента матриці з координатами $\left(i;j \right)$ позначається як $((A)_(ij))$ і вважається за схемою:

1. Спочатку викреслюємо з вихідної матриці $i$-рядок і $j$-й стовпець. Отримаємо нову квадратну матрицю і її визначник ми позначаємо як $M_(ij)^(*)$.
2. Потім множимо цей визначник на $((\left(-1 \right))^(i+j))$ — спочатку цей вираз може здатися мозковиносним, але по суті ми просто з'ясовуємо знак перед $M_(ij)^(*) $.
3. Вважаємо - отримуємо конкретне число. Тобто. Додаток алгебри — це саме число, а не якась нова матриця і т.д.

Саму матрицю $M_(ij)^(*)$ називають додатковим мінором до елемента $((a)_(ij))$. І в цьому сенсі наведене вище визначення алгебраїчного доповнення є окремим випадком складнішого визначення того, що ми розглядали в уроці про визначник.

Важливе зауваження. Загалом у «дорослій» математиці алгебраїчні доповнення визначаються так:

1. Беремо у квадратній матриці $k$ рядків і $k$ стовпців. На їх перетині вийде матриця розміру $ \ left [k \ times k \ right] $ - її визначник називається мінором порядку $ k $ і позначається $ ((M)_ (k)) $.
2. Потім викреслюємо ці «вибрані» $k$ рядків і $k$ стовпців. Знову вийде квадратна матриця - її визначник називається додатковим мінором і позначається $ M_(k) ^ (*) $.
3. Помножуємо $M_(k)^(*)$ на $((\left(-1 \right))^(t))$, де $t$ — це (ось зараз увага!) сума номерів усіх вибраних рядків та стовпців . Це і буде додаток алгебри.

Погляньте на третій крок: там взагалі сума $2k$ доданків! Інша річ, що для $k=1$ ми отримаємо лише 2 доданків — це будуть ті самі $i+j$ — «координати» елемента $((a)_(ij))$, для якого ми шукаємо алгебраїчне доповнення.

Таким чином, сьогодні ми використовуємо злегка спрощене визначення. Але як ми побачимо надалі, його виявиться більш ніж достатньо. Куди важливіша наступна штука:

Визначення. Союзна матриця $S$ до квадратної матриці $A=\left[ n\times n \right]$ — це нова матриця розміру $\left[ n\times n \right]$, яка виходить із $A$ заміною $(( a)_(ij))$ алгебраїчними доповненнями $((A)_(ij))$:

\\Rightarrow S=\left[ \begin(matrix) ((A)_(11)) & ((A)_(12)) & ... & ((A)_(1n)) \\ (( A)_(21)) & ((A)_(22)) & ... & ((A)_(2n)) \\ ... & ... & ... & ... \\ ((A)_(n1)) & ((A)_(n2)) & ... & ((A)_(nn)) \\\end(matrix) \right]\]

Перша думка, що виникає в момент усвідомлення цього визначення - це скільки ж доведеться всього вважати! Розслабтеся: вважати доведеться, але не так вже й багато.

Що ж, все це дуже мило, але навіщо це потрібне? А ось навіщо.

Основна теорема

Повернемося трохи тому. Пам'ятайте, в Лемме 3 стверджувалося, що оборотна матриця $A$ завжди не вироджена (тобто її визначник відмінний від нуля: $ \ left | A \ right | \ ne 0 $).

Так ось, вірно і зворотне: якщо матриця $ A $ не вироджена, вона завжди оборотна. І навіть існує схема пошуку $((A)^(-1))$. Зацініть:

Теорема про зворотну матрицю. Нехай дана квадратна матриця $ A = \ left [n \ times n \ right] $, причому її визначник відмінний від нуля: $ \ left | A \right|\ne 0$. Тоді зворотна матриця $((A)^(-1))$ існує і вважається за формулою:

\[((A)^(-1))=\frac(1)(\left| A \right|)\cdot ((S)^(T))\]

А тепер — все те саме, але розбірливим почерком. Щоб знайти зворотну матрицю, потрібно:

1. Порахувати визначник $ \ left | A \right|$ і переконатися, що він відмінний від нуля.
2. Скласти союзну матрицю $S$, тобто. порахувати 100500 додатків алгебри $((A)_(ij))$ і розставити їх на місці $((a)_(ij))$.
3. Транспонувати цю матрицю $S$, а потім помножити її на деяке число $q=(1)/(\left|A \right|)\;$.

І все! Зворотну матрицю $((A)^(-1))$ знайдено. Давайте подивимося на приклади:

\[\left[ \begin(matrix) 3 & 1 \\ 5 & 2 \\\end(matrix) \right]\]

Рішення. Перевіримо оборотність. Порахуємо визначник:

\[\left| A \right|=\left| \begin(matrix) 3 & 1 \\ 5 & 2 \\\end(matrix) \right|=3\cdot 2-1\cdot 5=6-5=1\]

Визначник відмінний від нуля. Значить, матриця оборотна. Складемо союзну матрицю:

Порахуємо додатки алгебри:

\[\begin(align) & ((A)_(11))=((\left(-1 \right))^(1+1))\cdot \left| 2 \right|=2; \\ ((A)_(12))=((\left(-1 \right))^(1+2))\cdot \left| 5 \right|=-5; \\ ((A)_(21))=((\left(-1 \right))^(2+1))\cdot \left| 1 \right|=-1; \\ & ((A)_(22))=((\left(-1 \right))^(2+2))\cdot \left| 3 \right|=3. \\ \end(align)\]

Зверніть увагу: визначники | 2 |, | 5 |, | 1 | та |3| - це саме визначники матриць розміру $ \ left [1 \ times 1 \ right] $, а не модулі. Тобто. якщо в визначниках стояли негативні числа, прибирати мінус не треба.

Отже, наша союзна матриця виглядає так:

\[((A)^(-1))=\frac(1)(\left| A \right|)\cdot ((S)^(T))=\frac(1)(1)\cdot ( (\left[ \begin(array)(*(35)(r)) 2 & -5 \\ -1 & 3 \\\end(array) \right])^(T))=\left[ \begin (array)(*(35)(r)) 2 & -1 \\ -5 & 3 \\\end(array) \right]\]

Ну от і все. Завдання вирішено.

Відповідь. $\left[ \begin(array)(*(35)(r)) 2 & -1 \\ -5 & 3 \\\end(array) \right]$

Завдання. Знайдіть зворотну матрицю:

\[\left[ \begin(array)(*(35)(r)) 1 & -1 & 2 \\ 0 & 2 & -1 \\ 1 & 0 & 1 \\end(array) \right] \]

Рішення. Знову вважаємо визначник:

\[\begin(align) & \left| \begin(array)(*(35)(r)) 1 & -1 & 2 \\ 0 & 2 & -1 \\ 1 & 0 & 1 \\end(array) \right|=\begin(matrix ) \left(1\cdot 2\cdot 1+\left(-1 \right)\cdot \left(-1 \right)\cdot 1+2\cdot 0\cdot 0 \right)- \\ -\left (2\cdot 2\cdot 1+\left(-1 \right)\cdot 0\cdot 1+1\cdot \left(-1 \right)\cdot 0 \right) \\end(matrix)= \ \ & =\left(2+1+0 \right)-\left(4+0+0 \right)=-1\ne 0. \\ \end(align)\]

Визначник відмінний від нуля - матриця оборотна. А ось зараз буде найжорсткіша: треба порахувати аж 9 (дев'ять, мати їх!) алгебраїчних доповнень. І кожне з них міститиме визначник $\left[2\times 2\right]$. Полетіли:

\[\begin(matrix) ((A)_(11))=((\left(-1 \right))^(1+1))\cdot \left| \begin(matrix) 2 & -1 \\ 0 & 1 \\\end(matrix) \right|=2; \((A)_(12))=((\left(-1 \right))^(1+2))\cdot \left| \begin(matrix) 0 & -1 \\ 1 & 1 \\\end(matrix) \right|=-1; \((A)_(13))=((\left(-1 \right))^(1+3))\cdot \left| \begin(matrix) 0 & 2 \\ 1 & 0 \\\end(matrix) \right|=-2; \\ ... \\ ((A)_(33))=((\left(-1 \right))^(3+3))\cdot \left| \begin(matrix) 1 & -1 \\ 0 & 2 \\\end(matrix) \right|=2; \\ \end(matrix)\]

Коротше, союзна матриця виглядатиме так:

Отже, зворотна матриця буде такою:

\[((A)^(-1))=\frac(1)(-1)\cdot \left[ \begin(matrix) 2 & -1 & -2 \\ 1 & -1 & -1 \\ -3 & 1 & 2 \\end(matrix) \right]=\left[ \begin(array)(*(35)(r))-2 & -1 & 3 \\ 1 & 1 & -1 \ \ 2 & 1 & -2 \\\end(array) \right]\]

Ось і все. Ось і відповідь.

Відповідь. $\left[ \begin(array)(*(35)(r)) -2 & -1 & 3 \\ 1 & 1 & -1 \\ 2 & 1 & -2 \\end(array) \right ]$

Як бачите, наприкінці кожного прикладу ми виконували перевірку. У зв'язку з цим важливе зауваження:

Не лінуйтеся виконувати перевірку. Помножте вихідну матрицю на знайдену зворотну - має вийти $E$.

Виконати цю перевірку набагато простіше та швидше, ніж шукати помилку у подальших обчисленнях, коли, наприклад, ви вирішуєте матричне рівняння.

Альтернативний спосіб

Як я і говорив, теорема про зворотну матрицю чудово працює для розмірів $ \ left [2 \ times 2 \ right] $ і $ \ left [3 \ times 3 \ right] $ (в останньому випадку - вже не так вже й "прекрасно" »), а ось для матриць великих розмірів починається прямий смуток.

Але не переживайте: є альтернативний алгоритм, за допомогою якого можна незворушно знайти зворотну хоч для матриці $ \ left [10 \ times 10 \ right] $. Але, як це часто буває, для розгляду цього алгоритму нам знадобиться невелика теоретична вступна.

Елементарні перетворення

Серед різноманітних перетворень матриці є кілька особливих їх називають елементарними. Таких перетворень рівно три:

1. множення. Можна взяти $i$-й рядок (стовпець) і помножити його на будь-яке число $k\ne 0$;
2. Додавання. Додати до $i$-го рядка (стовпця) будь-який інший $j$-й рядок (стовпець), помножений на будь-яке число $k\ne 0$ (можна, звичайно, і $k=0$, але який у цьому сенс ? Нічого не зміниться ж).
3. Перестановка. Взяти $i$-ю і $j$-ю рядки (стовпці) і поміняти місцями.

Чому ці перетворення називаються елементарними (для великих матриць вони виглядають не такими вже елементарними) і чому їх лише три ці питання виходять за рамки сьогоднішнього уроку. Тому не вдаватимемося в подробиці.

Важливо інше: всі ці збочення ми повинні виконувати над приєднаною матрицею. Так, так: ви не дочули. Зараз буде ще одне визначення – останнє у сьогоднішньому уроці.

Приєднана матриця

Напевно, у школі ви вирішували системи рівнянь методом складання. Ну, там, відняти з одного рядка інший, помножити якийсь рядок на число - ось це все.

Так ось: зараз буде все те саме, але вже «по-дорослому». Чи готові?

Визначення. Нехай дана матриця $ A = \ left [n \ times n \ right] $ і одинична матриця $ E $ такого ж розміру $ n $. Тоді приєднана матриця $ \ left [ A \ left | E \right. \right]$ — це нова матриця розміру $\left[ n\times 2n \right]$, яка виглядає так:

\[\left[ A\left| E \right. \right]=\left[ \begin(array)(rrrr|rrrr)((a)_(11)) & ((a)_(12)) & ... & ((a)_(1n)) & 1 & 0 & ... & 0 \\((a)_(21)) & ((a)_(22)) & ... & ((a)_(2n)) & 0 & 1 & ... & 0 \\... & ... & ... & ... & ... & ... & ... & ... \\((a)_(n1)) & ((a)_(n2)) & ... & ((a)_(nn)) & 0 & 0 & ... & 1 \\\end(array) \right]\]

Коротше кажучи, беремо матрицю $A$, праворуч приписуємо до неї одиничну матрицю $E$ потрібного розміру, розділяємо їх вертикальною рисою для краси - ось вам і приєднана.

У чому прикол? А ось у чому:

Теорема. Нехай матриця $A$ оборотна. Розглянемо приєднану матрицю $ \ left [ A \ left | E \right. \right]$. Якщо за допомогою елементарних перетворень рядківпривести її до вигляду $ \ left [ E \ left | B \right. \right]$, тобто. шляхом множення, віднімання та перестановки рядків отримати з $A$ матрицю $E$ праворуч, то отримана зліва матриця $B$ - це зворотна до $A$:

\[\left[ A\left| E \right. \right]\to \left[ E\left| B \right. \right]\Rightarrow B=((A)^(-1))\]

Ось так просто! Коротше кажучи, алгоритм знаходження зворотної матриці виглядає так:

1. Записати приєднану матрицю $\left[ A\left| E \right. \right]$;
2. Виконувати елементарні перетворення рядків доти, доки права замість $A$ не з'явиться $E$;
3. Зрозуміло, ліворуч теж щось з'явиться якась матриця $B$. Це і буде обернена;
4. PROFIT!:)

Звісно, ​​сказати набагато простіше, ніж зробити. Тому давайте розглянемо кілька прикладів: для розмірів $\left[ 3\times 3 \right]$ і $\left[ 4\times 4 \right]$.

Завдання. Знайдіть зворотну матрицю:

\[\left[ \begin(array)(*(35)(r)) 1 & 5 & 1 \\ 3 & 2 & 1 \\ 6 & -2 & 1 \\\end(array) \right]\ ]

Рішення. Складаємо приєднану матрицю:

\[\left[ \begin(array)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 3 & 2 & 1 & 0 & 1 & 0 \\ 6 & -2 & 1 & 0 & 0 & 1 \\\end(array) \right]\]

Оскільки останній стовпець вихідної матриці заповнений одиницями, віднімемо перший рядок з інших:

\[\begin(align) & \left[ \begin(array)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 3 & 2 & 1 & 0 & 1 & 0 \\ 6 & - 2 & 1 & 0 & 0 & 1 \endend(array) \right]\begin(matrix) \downarrow \\ -1 \\ -1 \\end(matrix)\to \\ & \to \left [ \begin(array)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 5 & -7 & 0 & -1 & 0 & 1 \\\end(array) \right] \\ \end(align)\]

Більше одиниць немає, окрім першого рядка. Але її ми не чіпаємо, інакше в третьому стовпці почнуть «розмножуватися» щойно прибрані одиниці.

Зате можемо відняти другий рядок двічі з останнього — отримаємо одиницю в нижньому лівому кутку:

\[\begin(align) & \left[ \begin(array)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 5 &-7 & 0 & -1 & 0 & 1 \endend(array) \right]\begin(matrix) \\ \downarrow \\ -2 \\end(matrix)\to \\ & \left [ \begin(array)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\end(array) \right] \\ \end(align)\]

Тепер можна відняти останній рядок з першого і двічі з другого — таким чином ми «занулимо» перший стовпець:

\[\begin(align) & \left[ \begin(array)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 1 & -1 & 0 & 1 & -2 & 1 \end(array) \right]\begin(matrix) -1 \\ -2 \\ \uparrow \\end(matrix)\to \ \ \ to \left[ \begin(array)(rrr|rrr) 0 & 6 & 1 & 0 & 2 & -1 \\ 0 & -1 & 0 & -3 & 5 & -2 \\ 1 & -1 & 0 & 1 & -2 & 1 \\end(array) \right] \\ \end(align)\]

Помножимо другий рядок на −1, а потім віднімемо його 6 разів з першого і додамо 1 раз до останнього:

\[\begin(align) & \left[ \begin(array)(rrr|rrr) 0 & 6 & 1 & 0 & 2 & -1 \\ 0 & -1 & 0 & -3 & 5 & -2 \ \ 1 & -1 & 0 & 1 & -2 & 1 \\end(array) \right]\begin(matrix) \ \\ \left| \cdot \left(-1 \right) \right. \\ \\\end(matrix)\to \\ & \to \left[ \begin(array)(rrr|rrr) 0 & 6 & 1 & 0 & 2 & -1 \\ 0 & 1 & 0 & 3 & -5 & 2 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\end(array) \right]\begin(matrix) -6 \\ \updownarrow \\ +1 \\\end (matrix) \to \\ & \to \left[ \begin(array)(rrr|rrr) 0 & 0 & 1 & -18 & 32 & -13 \\ 0 & 1 & 0 & 3 & -5 & 2 \\ 1 & 0 & 0 & 4 & -7 & 3 \\end(array) \right] \\ \end(align)\]

Залишилося лише поміняти місцями рядки 1 та 3:

\[\left[ \begin(array)(rrr|rrr) 1 & 0 & 0 & 4 & -7 & 3 \\ 0 & 1 & 0 & 3 & -5 & 2 \\ 0 & 0 & 1 & - 18 & 32 & -13 \\end(array) \right]\]

Готово! Праворуч - шукана зворотна матриця.

Відповідь. $\left[ \begin(array)(*(35)(r))4 & -7 & 3 \\ 3 & -5 & 2 \\ -18 & 32 & -13 \\end(array) \right ]$

Завдання. Знайдіть зворотну матрицю:

\[\left[ \begin(matrix) 1 & 4 & 2 & 3 \\ 1 & -2 & 1 & -2 \\ 1 & -1 & 1 & 1 \\ 0 & -10 & -2 & -5 \\end(matrix) \right]\]

Рішення. Знову складаємо приєднану:

\[\left[ \begin(array)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 1 & -2 & 1 & -2 & 0 & 1 & 0 & 0 \ \ 1 & -1 & 1 & 1 & 0 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\\end(array) \right]\]

Трохи позалимаємо, потурбуємося від того, скільки зараз доведеться рахувати... і почнемо рахувати. Для початку «обнулили» перший стовпець, віднімаючи рядок 1 з рядків 2 та 3:

\[\begin(align) & \left[ \begin(array)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 1 & -2 & 1 & -2 & 0 & 1 & 0 & 0 \\ 1 & -1 & 1 & 1 & 0 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\end(array) \right]\begin(matrix) \downarrow \\ -1 \\ -1 \\ \\\end(matrix)\to \\ & \to \left[ \begin(array)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 0 & -6 & -1 & -5 & -1 & 1 & 0 & 0 \\ 0 & -5 & -1 & -2 & -1 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\\end(array) \right] \\ \end(align)\]

Спостерігаємо дуже багато «мінусів» у рядках 2—4. Помножимо всі три рядки на −1, а потім випалимо третій стовпець, віднімаючи рядок 3 з інших:

\[\begin(align) & \left[ \begin(array)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 0 & -6 & -1 & -5 & - 1 & 1 & 0 & 0 \\ 0 & -5 & -1 & -2 & -1 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\ \end(array) \right]\begin(matrix) \ \\ \left| \cdot \left(-1 \right) \right. \\ \left| \cdot \left(-1 \right) \right. \\ \left| \cdot \left(-1 \right) \right. \\\end(matrix)\to \\ & \to \left[ \begin(array)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 0 & 6 & 1 & 5 & ​​1 & -1 & 0 & 0 \\ 0 & 5 & 1 & 2 & 1 & 0 & -1 & 0 \\ 0 & 10 & 2 & 5 & 0 & 0 & 0 & -1 \\\end (array) \right]\begin(matrix) -2 \\ -1 \\ \updownarrow \\ -2 \\end(matrix)\to \\ & \to \left[ \begin(array)(rrrr| rrrr) 1 & -6 & 0 & -1 & -1 & 0 & 2 & 0 \\ 0 & 1 & 0 & 3 & 0 & -1 & 1 & 0 \\ 0 & 5 & 1 & 2 & 1 & 0 & -1 & 0 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\end(array) \right] \\ \end(align)\]

Тепер саме час «підсмажити» останній стовпець вихідної матриці: віднімаємо рядок 4 з інших:

\[\begin(align) & \left[ \begin(array)(rrrr|rrrr) 1 & -6 & 0 & -1 & -1 & 0 & 2 & 0 \\ 0 & 1 & 0 & 3 & 0 & -1 & 1 & 0 \\ 0 & 5 & 1 & 2 & 1 & 0 & -1 & 0 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\end(array ) \right]\begin(matrix) +1 \\ -3 \\ -2 \\ \uparrow \\end(matrix)\to \\ & \to \left[ \begin(array)(rrrr|rrrr) 1 & -6 & 0 & 0 & -3 & 0 & 4 & -1 \\ 0 & 1 & 0 & 0 & 6 & -1 & -5 & 3 \\ 0 & 5 & 1 & 0 & 5 & 0 & -5 & 2 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end(array) \right] \\ \end(align)\]

Фінальний кидок: «випалюємо» другий стовпець, віднімаючи рядок 2 з рядка 1 та 3:

\[\begin(align) & \left[ \begin(array)(rrrr|rrrr) 1 & -6 & 0 & 0 & -3 & 0 & 4 & -1 \\ 0 & 1 & 0 & 0 & 6 & -1 & -5 & 3 \\ 0 & 5 & 1 & 0 & 5 & 0 & -5 & 2 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\end( array) \right]\begin(matrix) 6 \\ \updownarrow \\ -5 \\ \\end(matrix)\to \\ & \to \left[ \begin(array)(rrrr|rrrr) 1 & 0 & 0 & 0 & 33 & -6 & -26 & -17 \\ 0 & 1 & 0 & 0 & 6 & -1 & -5 & 3 \\ 0 & 0 & 1 & 0 & -25 & 5 & 20 & -13 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\end(array) \right] \\ \end(align)\]

І знову зліва одинична матриця, значить праворуч - зворотна.:)

Відповідь. $\left[ \begin(matrix) 33 & -6 & -26 & 17 \\ 6 & -1 & -5 & 3 \\ -25 & 5 & 20 & -13 \\ -2 & 0 & 2 & - 1 \\\end(matrix) \right]$

Ну от і все. Перевірку зробіть самі - мені в лом.

Подібні на зворотні за багатьма властивостями.

Енциклопедичний YouTube

1 / 5

✪ Зворотна матриця (2 способи знаходження)

✪ Як знаходити зворотну матрицю - bezbotvy

✪ Зворотня матриця #1

✪ Вирішення системи рівнянь методом зворотної матриці - bezbotvy

✪ Зворотна Матриця

Субтитри

Властивості зворотної матриці

• det A − 1 = 1 det A (\displaystyle \det A^(-1)=(\frac (1)(\det A))), де det (\displaystyle \ \det )позначає визначник.
• (A B) − 1 = B − 1 A − 1 (\displaystyle \ (AB)^(-1)=B^(-1)A^(-1))для двох квадратних оборотних матриць A (\displaystyle A)і B (\displaystyle B).
• (A T) − 1 = (A − 1) T (\displaystyle \ (A^(T))^(-1)=(A^(-1))^(T)), де (. . .) T (\displaystyle (...)^(T))позначає транспоновану матрицю.
• (k A) − 1 = k − 1 A − 1 (\displaystyle \ (kA)^(-1)=k^(-1)A^(-1))для будь-якого коефіцієнта k ≠ 0 (\displaystyle k\not = 0).
• E − 1 = E (\displaystyle \ E^(-1)=E).
• Якщо необхідно вирішити систему лінійних рівнянь , (b - ненульовий вектор) де x (\displaystyle x)- Шуканий вектор, і якщо A − 1 (\displaystyle A^(-1))існує, то x = A − 1 b (\displaystyle x=A^(-1)b). В іншому випадку або розмірність простору рішень більша за нуль, або їх немає зовсім.

Способи знаходження зворотної матриці

Якщо матриця оборотна, то для знаходження зворотної матриці можна скористатися одним із наступних способів:

Точні (прямі) методи

Метод Гауса-Жордана

Візьмемо дві матриці: саму Aта одиничну E. Наведемо матрицю Aдо одиничної матриці методом Гаусса-Жордана застосовуючи перетворення по рядках (можна також застосовувати перетворення і по стовпцях, але не в перемішування). Після застосування кожної операції до першої матриці застосуємо ту саму операцію до другої. Коли приведення першої матриці до одиничного вигляду буде завершено, друга матриця виявиться рівною. A −1.

При використанні методу Гауса перша матриця збільшуватиметься зліва на одну з елементарних матриць Λ i (\displaystyle \Lambda _(i))(трансвекцію або діагональну матрицю з одиницями на головній діагоналі, крім однієї позиції):

Λ 1 ⋅ ⋯ ⋅ Λ n ⋅ A = Λ A = E ⇒ Λ = A − 1 (\displaystyle \Lambda _(1)\cdot \dots \cdot \Lambda _(n)\cdot A=\Lambda A=E \Rightarrow \Lambda =A^(-1)). Λ m = [ 1 … 0 − a 1 m / a m m 0 … 0 … 0 … 1 – a m − 1 m / a m m 0 … 0 0 … 0 1 / a m m 0 … 0 0 … 0 – a m + 1 m / a m m … 0 … 0 … 0 − a n m / a m m 0 … 1 ] (\displaystyle \Lambda _(m)=(\begin(bmatrix)1&\dots &0&-a_(1m)/a_(mm)&0&\dots &0\\ &&&\dots &&&\\0&\dots &1&-a_(m-1m)/a_(mm)&0&\dots &0\\0&\dots &0&1/a_(mm)&0&\dots &0\\0&\dots &0&-a_( m+1m)/a_(mm)&1&\dots &0\\&&&\dots &&&\\0&\dots &0&-a_(nm)/a_(mm)&0&\dots &1\end(bmatrix))).

Друга матриця після застосування всіх операцій дорівнюватиме Λ (\displaystyle \Lambda )тобто буде шуканою. Складність алгоритму - O (n 3) (\displaystyle O(n^(3))).

За допомогою матриці додатків алгебри

Матриця, обернена матриці A (\displaystyle A), представна у вигляді

A − 1 = adj (A) det (A) (\displaystyle (A)^(-1)=(((\mbox(adj))(A)) \over (\det(A))))

де adj (A) (\displaystyle (\mbox(adj))(A))- приєднана матриця;

Складність алгоритму залежить від складності алгоритму розрахунку визначника O det і дорівнює O(n²) · O det.

Використання LU/LUP-розкладання

Матричне рівняння A X = I n (\displaystyle AX = I_(n))для зворотної матриці X (\displaystyle X)можна розглядати як сукупність n (\displaystyle n)систем виду A x = b (\displaystyle Ax = b). Позначимо i (\displaystyle i)-ий стовпець матриці X (\displaystyle X)через X i (\displaystyle X_(i)); тоді A X i = e i (\displaystyle AX_(i)=e_(i)), i = 1, …, n (\displaystyle i = 1, \ ldots, n),оскільки i (\displaystyle i)-м стовпцем матриці I n (\displaystyle I_(n))є одиничний вектор e i (\displaystyle e_(i)). іншими словами, перебування зворотної матриці зводиться до розв'язання n рівнянь з однією матрицею та різними правими частинами. Після виконання LUP-розкладання (час O(n³)) на розв'язання кожного з n рівнянь потрібен час O(n²), так що і ця частина роботи потребує часу O(n³).

Якщо матриця A невироджена, то нею можна розрахувати LUP-разложение P A = L U (\displaystyle PA = LU). Нехай P A = B (\displaystyle PA = B), B − 1 = D (\displaystyle B^(-1)=D). Тоді із властивостей зворотної матриці можна записати: D = U − 1 L − 1 (\displaystyle D=U^(-1)L^(-1)). Якщо помножити цю рівність на U і L можна отримати дві рівності виду U D = L − 1 (\displaystyle UD=L^(-1))і DL = U − 1 (\displaystyle DL=U^(-1)). Перша з цих рівностей є системою з n² лінійних рівнянь для n (n + 1) 2 (\displaystyle (\frac (n(n+1))(2)))з яких відомі праві частини (з властивостей трикутних матриць). Друге представляє також систему з n² лінійних рівнянь для n (n − 1) 2 (\displaystyle (\frac (n(n-1))(2)))з яких відомі праві частини (також із властивостей трикутних матриць). Разом вони є системою з n² рівностей. За допомогою цих рівностей можна реккурентно визначити всі n² елементів матриці D. Тоді з рівності (PA) −1 = A −1 P −1 = B −1 = D. отримуємо рівність A − 1 = DP (\displaystyle A^(-1)=DP).

У разі використання LU-розкладання не потрібно перестановки стовпців матриці D, але рішення може розійтися навіть якщо матриця A невироджена.

Складність алгоритму – O(n³).

Ітераційні методи

Методи Шульця

( Ψ k = E − A U k , U k + 1 = U k ∑ i = 0 n Ψ k i (\displaystyle (\begin(cases)\Psi _(k)=E-AU_(k),\\U_( k+1)=U_(k)\sum _(i=0)^(n)\Psi _(k)^(i)\end(cases)))

Оцінка похибки

Вибір початкового наближення

Проблема вибору початкового наближення в аналізованих тут процесах ітераційного звернення матриць не дозволяє ставитися до них як до самостійних універсальних методів, що конкурують із прямими методами обігу, заснованими, наприклад, на LU-розкладанні матриць. Є деякі рекомендації щодо вибору U 0 (\displaystyle U_(0)), що забезпечують виконання умови ρ (Ψ 0) < 1 {\displaystyle \rho (\Psi _{0})<1} (спектральний радіус матриці менше одиниці), що є необхідним та достатнім для збіжності процесу. Однак при цьому, по-перше, потрібно знати зверху оцінку спектра матриці, що звертається, A або матриці AT (\displaystyle AA^(T))(а саме, якщо A - симетрична позитивно визначена матриця та ρ (A) ≤ β (\displaystyle \rho (A)\leq \beta ), то можна взяти U 0 = α E (\displaystyle U_(0)=(\alpha )E), де; якщо ж A - довільна невироджена матриця та ρ (A A T) ≤ β (\displaystyle \rho (AA^(T))\leq \beta ), то вважають U 0 = α A T (\displaystyle U_(0)=(\alpha )A^(T)), де також α ∈ (0 , 2 β) (\displaystyle \alpha \in \left(0,(\frac (2)(\beta ))\right)); можна звичайно спростити ситуацію і, скориставшись тим, що ρ (A A T) ≤ k A A T k (\displaystyle \rho (AA^(T))\leq (\mathcal (k))AA^(T)(\mathcal (k))), покласти U 0 = A T ‖ A A T ‖ (\displaystyle U_(0)=(\frac (A^(T))(\|AA^(T)\|)))). По-друге, за такого завдання початкової матриці немає гарантії, що ‖ Ψ 0 ‖ (\displaystyle \|\Psi _(0)\|)буде малою (можливо, навіть виявиться ‖ Ψ 0 ‖ > 1 (\displaystyle \|\Psi _(0)\|>1)), і високий порядок швидкості збіжності виявиться далеко ще не відразу.

Приклади

Матриця 2х2

Неможливо розібрати вираз (синтаксична помилка): (\displaystyle \mathbf(A)^(-1) = \begin(bmatrix) a & b \\ c & d \end(bmatrix)^(-1) = \frac (1)(\det(\mathbf(A))) \begin& \!\!-b \\ -c & \,a \\ \end(bmatrix) = \frac(1)(ad - bc) \begin (bmatrix) \,\,\,d & \!\!-b\\ -c & \,a \end(bmatrix).

Звернення матриці 2х2 можливе лише за умови, що a d − b c = det A ≠ 0 (\displaystyle ad-bc=\det A\neq 0).

Для вирішення системи лінійних рівнянь (3) щодо x 1скористаємося методом Гаусса.

Аналогічним чином вирішуються інші системи лінійних рівнянь (2).

Нарешті, група векторів стовпців. x 1 , x 2 , ..., x nутворює зворотну матрицю A -1.

Зауважимо, що один раз знаходячи матриці перестановок P 1 ,P 2 , ... , P n-1та матриці винятків М 1, М 2, ..., M n-1(див. сторінку Метод виключення Гауса) та побудувавши матрицю

M = M n-1 P n-1 ... M 2 P 2 M 1 P 1 ,

систему (2) можна перетворити на вигляд

• MAx 1 = Me 1 ,
• MAx 2 = Me 2 ,
• ......
• MAx n = Me n .

Звідси перебувають x 1, x 2, ..., x n, за різних правих частин Me 1, Me 2, ..., Me n.

При обчисленні зворотної матриці зручніше праворуч вихідної матриці додати одиничну матрицю і застосовувати метод Гауса в прямому і зворотному напрямках.

Розглянемо це з прикладу.

Приклад обчислення зворотної матриці

Нехай потрібно знайти зворотну матрицю A -1для даної матриці A:

Запишемо з правого боку поодиноку матрицю:

Вибираємо провідний елемент "4" (т.к. він найбільший за модулем) і переставляємо місцями перший і третій рядки:

Застосовуємо Гауссове виняток для першого стовпця:

Переставляємо другий і третій рядки і застосовуємо Гауссів виняток для другого стовпця.