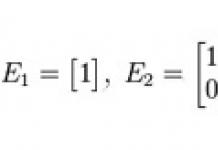Mencari matriks invers menggunakan determinan. Algoritma untuk menghitung matriks invers. Transformasi matriks dasar

Misalkan ada matriks persegi orde ke-n

Matriks A -1 disebut matriks terbalik terhadap matriks A, jika A*A -1 = E, dimana E adalah matriks identitas orde ke-n.

Matriks identitas- matriks persegi yang semua elemen sepanjang diagonal utama, dari sudut kiri atas ke sudut kanan bawah, adalah satu, dan sisanya adalah nol, misalnya:

matriks terbalik mungkin ada hanya untuk matriks persegi itu. untuk matriks-matriks yang jumlah baris dan kolomnya berhimpitan.

Teorema kondisi keberadaan matriks invers

Agar suatu matriks memiliki matriks invers, matriks tersebut perlu dan cukup bersifat non-singular.

Matriks A = (A1, A2,...A n) disebut tidak merosot, jika vektor kolom bebas linier. Banyaknya vektor kolom bebas linier suatu matriks disebut pangkat matriks. Oleh karena itu, kita dapat mengatakan bahwa agar suatu matriks invers ada, pangkat matriks tersebut perlu dan cukup sama dengan dimensinya, yaitu. r = n.

Algoritma untuk mencari matriks invers

Tuliskan matriks A ke dalam tabel untuk menyelesaikan sistem persamaan menggunakan metode Gaussian dan tetapkan matriks E di sebelah kanannya (sebagai pengganti ruas kanan persamaan).
Dengan menggunakan transformasi Jordan, reduksi matriks A menjadi matriks yang terdiri dari kolom satuan; dalam hal ini perlu dilakukan transformasi matriks E secara simultan.
Jika perlu, susun ulang baris-baris (persamaan) tabel terakhir sehingga di bawah matriks A tabel asal diperoleh matriks identitas E.
Tuliskan invers matriks A -1 yang terletak pada tabel terakhir di bawah matriks E tabel asal.

Contoh 1

Untuk matriks A, carilah invers matriks A -1

Solusi: Kita tuliskan matriks A dan letakkan matriks identitas E di sebelah kanan. Dengan menggunakan transformasi Jordan, kita mereduksi matriks A menjadi matriks identitas E. Perhitungannya diberikan pada Tabel 31.1.

Mari kita periksa kebenaran perhitungannya dengan mengalikan matriks asli A dan matriks invers A -1.

Hasil perkalian matriks diperoleh matriks identitas. Oleh karena itu, perhitungan dilakukan dengan benar.

Menjawab:

Memecahkan persamaan matriks

Persamaan matriks dapat terlihat seperti:

KAPAK = B, HA = B, AXB = C,

dimana A, B, C adalah matriks yang ditentukan, X adalah matriks yang diinginkan.

Persamaan matriks diselesaikan dengan mengalikan persamaan tersebut dengan matriks invers.

Misalnya, untuk mencari matriks dari persamaan, Anda perlu mengalikan persamaan ini dengan persamaan di sebelah kiri.

Oleh karena itu, untuk mencari solusi persamaan tersebut, Anda perlu mencari matriks invers dan mengalikannya dengan matriks di sisi kanan persamaan.

Persamaan lainnya diselesaikan dengan cara yang sama.

Contoh 2

Selesaikan persamaan AX = B jika

Larutan: Karena invers matriksnya sama dengan (lihat contoh 1)

Metode matriks dalam analisis ekonomi

Selain yang lain, mereka juga digunakan metode matriks. Metode ini didasarkan pada aljabar linier dan matriks vektor. Metode tersebut digunakan untuk tujuan menganalisis fenomena ekonomi yang kompleks dan multidimensi. Paling sering, metode ini digunakan ketika diperlukan untuk melakukan penilaian komparatif terhadap fungsi organisasi dan divisi strukturalnya.

Dalam proses penerapan metode analisis matriks, dapat dibedakan beberapa tahapan.

Pada tahap pertama suatu sistem indikator ekonomi sedang dibentuk dan atas dasar itu disusun matriks data awal, yang merupakan tabel di mana nomor-nomor sistem ditampilkan dalam baris-baris individualnya (saya = 1,2,....,n), dan di kolom vertikal - jumlah indikator (j = 1,2,....,m).

Pada tahap kedua Untuk setiap kolom vertikal, nilai indikator terbesar yang tersedia diidentifikasi, yang diambil sebagai satu.

Setelah itu, semua jumlah yang tercermin dalam kolom ini dibagi dengan nilai terbesar dan matriks koefisien standar terbentuk.

Pada tahap ketiga semua komponen matriks dikuadratkan. Jika mempunyai signifikansi yang berbeda, maka setiap indikator matriks diberi koefisien bobot tertentu k. Nilai yang terakhir ditentukan oleh pendapat para ahli.

Yang terakhir, tahap keempat nilai peringkat yang ditemukan Rj dikelompokkan berdasarkan kenaikan atau penurunannya.

Metode matriks yang diuraikan harus digunakan, misalnya, dalam analisis komparatif berbagai proyek investasi, serta dalam menilai indikator ekonomi lainnya dari kegiatan organisasi.

Untuk setiap matriks non-tunggal A terdapat matriks unik A -1 sedemikian rupa sehingga

A*A -1 =A -1 *A = E,

dimana E adalah matriks identitas yang berorde sama dengan A. Matriks A -1 disebut invers dari matriks A.

Kalau ada yang lupa, pada matriks identitas, kecuali diagonalnya diisi satu, semua posisi lainnya diisi nol, contoh matriks identitas:

Mencari matriks invers menggunakan metode matriks adjoint

Matriks invers ditentukan dengan rumus:

dimana A ij - elemen a ij.

Itu. Untuk menghitung matriks invers, Anda perlu menghitung determinan matriks tersebut. Kemudian temukan komplemen aljabar untuk semua elemennya dan buat matriks baru dari elemen tersebut. Selanjutnya Anda perlu memindahkan matriks ini. Dan membagi setiap elemen matriks baru dengan determinan matriks asal.

Mari kita lihat beberapa contoh.

Temukan A -1 untuk sebuah matriks

Solusi Mari kita cari A -1 menggunakan metode matriks adjoint. Kita mempunyai det A = 2. Mari kita cari komplemen aljabar elemen-elemen matriks A. Dalam hal ini, komplemen aljabar elemen-elemen matriks adalah elemen-elemen yang bersesuaian dari matriks itu sendiri, diambil dengan tanda sesuai dengan rumus

Kita mempunyai A 11 = 3, A 12 = -4, A 21 = -1, A 22 = 2. Kita membentuk matriks adjoint

Kami mengangkut matriks A*:

Kita mencari matriks inversnya menggunakan rumus:

Kita mendapatkan:

Dengan menggunakan metode matriks adjoin, carilah A -1 jika

Solusi Pertama-tama, kita menghitung definisi matriks ini untuk memverifikasi keberadaan matriks invers. Kita punya

Di sini kita menambahkan elemen baris kedua ke elemen baris ketiga, yang sebelumnya dikalikan (-1), dan kemudian memperluas determinan baris kedua. Karena definisi matriks ini bukan nol, maka matriks inversnya ada. Untuk membangun matriks adjoin, kita mencari komplemen aljabar dari elemen-elemen matriks ini. Kita punya

Menurut rumusnya

matriks transportasi A*:

Kemudian sesuai rumus

Mencari matriks invers menggunakan metode transformasi elementer

Selain cara mencari matriks invers berdasarkan rumusnya (metode matriks adjoint), terdapat metode mencari matriks invers yang disebut metode transformasi elementer.

Transformasi matriks dasar

Transformasi berikut disebut transformasi matriks dasar:

1) penataan ulang baris (kolom);

2) mengalikan suatu baris (kolom) dengan bilangan selain nol;

3) menjumlahkan unsur-unsur suatu baris (kolom) unsur-unsur yang bersesuaian pada baris (kolom) yang lain, yang sebelumnya dikalikan dengan suatu bilangan tertentu.

Untuk mencari matriks A -1, kita membuat matriks persegi panjang B = (A|E) berorde (n; 2n), menugaskan matriks A di sebelah kanan matriks identitas E melalui garis pemisah:

Mari kita lihat sebuah contoh.

Dengan menggunakan metode transformasi elementer, carilah A -1 jika

Solusi Mari kita bentuk matriks B:

Mari kita nyatakan baris-baris matriks B dengan α 1, α 2, α 3. Mari kita lakukan transformasi berikut pada baris matriks B.

Topik ini adalah salah satu yang paling dibenci di kalangan siswa. Yang lebih buruk, mungkin, adalah kualifikasi.

Triknya adalah konsep elemen invers (dan saya tidak hanya berbicara tentang matriks) merujuk kita pada operasi perkalian. Bahkan dalam kurikulum sekolah, perkalian dianggap sebagai operasi yang kompleks, dan perkalian matriks umumnya merupakan topik terpisah, yang saya dedikasikan seluruh paragraf dan video pelajarannya.

Hari ini kita tidak akan membahas detail perhitungan matriks. Mari kita ingat saja: bagaimana matriks dilambangkan, bagaimana matriks tersebut dikalikan, dan apa yang berikut ini.

Ulasan: Perkalian Matriks

Pertama-tama, mari kita sepakati notasi. Matriks $A$ berukuran $\left[ m\times n \right]$ hanyalah sebuah tabel bilangan yang memiliki $m$ baris dan $n$ kolom yang tepat:

\=\underbrace(\left[ \begin(matriks) ((a)_(11)) & ((a)_(12)) & ... & ((a)_(1n)) \\ (( a)_(21)) & ((a)_(22)) & ... & ((a)_(2n)) \\ ... & ... & ... & ... \\ ((a)_(m1)) & ((a)_(m2)) & ... & ((a)_(mn)) \\\end(matriks) \kanan])_(n)\]

Untuk menghindari tercampurnya baris dan kolom secara tidak sengaja (percayalah, dalam ujian Anda bisa bingung antara satu dan dua, apalagi beberapa baris), lihat saja gambarnya:

Menentukan indeks untuk sel matriks

Apa yang terjadi? Jika Anda menempatkan sistem koordinat standar $OXY$ di sudut kiri atas dan mengarahkan sumbu sehingga menutupi seluruh matriks, maka setiap sel matriks ini dapat dikaitkan secara unik dengan koordinat $\left(x;y \right)$ - ini akan menjadi nomor baris dan nomor kolom.

Mengapa sistem koordinat ditempatkan di pojok kiri atas? Ya, karena dari situlah kita mulai membaca teks apa pun. Sangat mudah untuk mengingatnya.

Mengapa sumbu $x$ mengarah ke bawah dan bukan ke kanan? Sekali lagi, sederhana saja: ambil sistem koordinat standar (sumbu $x$ ke kanan, sumbu $y$ ke atas) dan putar sehingga menutupi matriks. Ini adalah rotasi 90 derajat searah jarum jam - kita melihat hasilnya pada gambar.

Secara umum, kita telah mengetahui cara menentukan indeks elemen matriks. Sekarang mari kita lihat perkalian.

Definisi. Matriks $A=\left[ m\times n \right]$ dan $B=\left[ n\times k \right]$, jika jumlah kolom pada kolom pertama sama dengan jumlah baris pada kolom kedua, adalah disebut konsisten.

Tepat dalam urutan itu. Kita mungkin bingung dan mengatakan bahwa matriks $A$ dan $B$ membentuk pasangan terurut $\left(A;B \right)$: jika matriks-matriks tersebut konsisten dalam urutan ini, maka $B sama sekali tidak perlu $ dan $A$ itu. pasangan $\left(B;A \right)$ juga konsisten.

Hanya matriks yang cocok yang dapat dikalikan.

Definisi. Hasil kali matriks $A=\left[ m\times n \right]$ dan $B=\left[ n\times k \right]$ adalah matriks baru $C=\left[ m\times k \right ]$ , yang elemennya $((c)_(ij))$ dihitung berdasarkan rumus:

\[((c)_(ij))=\jumlah\batas_(k=1)^(n)(((a)_(ik)))\cdot ((b)_(kj))\]

Dengan kata lain: untuk mendapatkan elemen $((c)_(ij))$ dari matriks $C=A\cdot B$, Anda perlu mengambil baris $i$ dari matriks pertama, $j$ -kolom matriks kedua, lalu mengalikan elemen-elemen dari baris dan kolom ini secara berpasangan. Jumlahkan hasilnya.

Ya, itu definisi yang kasar. Beberapa fakta segera menyusul darinya:

Perkalian matriks, secara umum, bersifat non-komutatif: $A\cdot B\ne B\cdot A$;
Namun, perkalian bersifat asosiatif: $\left(A\cdot B \right)\cdot C=A\cdot \left(B\cdot C \right)$;
Dan bahkan secara distribusi: $\left(A+B \right)\cdot C=A\cdot C+B\cdot C$;
Dan sekali lagi secara distributif: $A\cdot \left(B+C \right)=A\cdot B+A\cdot C$.

Distributivitas perkalian harus dijelaskan secara terpisah untuk faktor penjumlahan kiri dan kanan justru karena operasi perkalian tidak bersifat komutatif.

Jika ternyata $A\cdot B=B\cdot A$, matriks tersebut disebut komutatif.

Di antara semua matriks yang dikalikan dengan sesuatu di sana, ada matriks khusus - matriks yang, jika dikalikan dengan matriks $A$, menghasilkan $A$ lagi:

Definisi. Matriks $E$ disebut identitas jika $A\cdot E=A$ atau $E\cdot A=A$. Dalam kasus matriks persegi $A$ kita dapat menulis:

Matriks identitas sering menjadi tamu ketika menyelesaikan persamaan matriks. Dan secara umum sering menjadi tamu di dunia matriks. :)

Dan karena $E$ ini, seseorang mengemukakan semua omong kosong yang akan ditulis selanjutnya.

Apa itu matriks invers

Karena perkalian matriks adalah operasi yang sangat memakan waktu (Anda harus mengalikan sekumpulan baris dan kolom), konsep matriks invers juga bukanlah yang paling sepele. Dan membutuhkan penjelasan.

Definisi Kunci

Nah, inilah waktunya untuk mengetahui kebenarannya.

Definisi. Matriks $B$ disebut invers matriks $A$ jika

Matriks invers dilambangkan dengan $((A)^(-1))$ (jangan disamakan dengan derajat!), sehingga definisinya dapat ditulis ulang sebagai berikut:

Tampaknya semuanya sangat sederhana dan jelas. Namun ketika menganalisis definisi ini, beberapa pertanyaan langsung muncul:

Apakah matriks invers selalu ada? Dan jika tidak selalu, lalu bagaimana menentukan: kapan ada dan kapan tidak?
Dan siapa bilang hanya ada satu matriks seperti itu? Bagaimana jika untuk matriks awal $A$ terdapat banyak invers?
Seperti apa semua “kebalikan” ini? Dan bagaimana tepatnya kita menghitungnya?

Mengenai algoritma perhitungan, kita akan membicarakannya nanti. Tapi kami akan menjawab pertanyaan yang tersisa sekarang. Mari kita rumuskan dalam bentuk pernyataan-lemma tersendiri.

Properti dasar

Mari kita mulai dengan bagaimana matriks $A$ seharusnya, pada prinsipnya, terlihat agar $((A)^(-1))$ ada untuk matriks tersebut. Sekarang kita akan memastikan bahwa kedua matriks ini harus berbentuk persegi, dan berukuran sama: $\left[ n\times n \right]$.

Lemma 1. Diberikan matriks $A$ dan inversnya $((A)^(-1))$. Maka kedua matriks ini berbentuk persegi, dan berorde $n$ yang sama.

Bukti. Itu mudah. Misalkan matriks $A=\left[ m\times n \right]$, $((A)^(-1))=\left[ a\times b \right]$. Karena produk $A\cdot ((A)^(-1))=E$ ada menurut definisi, matriks $A$ dan $((A)^(-1))$ konsisten dalam urutan yang ditunjukkan:

\[\begin(align) & \left[ m\times n \right]\cdot \left[ a\times b \right]=\left[ m\times b \right] \\ & n=a \end( meluruskan)\]

Ini adalah konsekuensi langsung dari algoritma perkalian matriks: koefisien $n$ dan $a$ adalah “transit” dan harus sama.

Pada saat yang sama, perkalian invers juga didefinisikan: $((A)^(-1))\cdot A=E$, oleh karena itu matriks $((A)^(-1))$ dan $A$ adalah juga konsisten dalam urutan yang ditentukan:

\[\begin(align) & \left[ a\times b \right]\cdot \left[ m\times n \right]=\left[ a\times n \right] \\ & b=m \end( meluruskan)\]

Jadi, tanpa kehilangan sifat umum, kita dapat berasumsi bahwa $A=\left[ m\times n \right]$, $((A)^(-1))=\left[ n\times m \right]$. Namun, menurut definisi $A\cdot ((A)^(-1))=((A)^(-1))\cdot A$, maka ukuran matriksnya sama persis:

\[\begin(align) & \left[ m\times n \right]=\left[ n\times m \right] \\ & m=n \end(align)\]

Jadi ternyata ketiga matriks - $A$, $((A)^(-1))$ dan $E$ - adalah matriks persegi berukuran $\left[ n\times n \right]$. Lemmanya terbukti.

Yah, itu sudah bagus. Kita melihat bahwa hanya matriks persegi yang dapat dibalik. Sekarang mari kita pastikan matriks inversnya selalu sama.

Lemma 2. Diberikan matriks $A$ dan inversnya $((A)^(-1))$. Maka matriks invers ini adalah satu-satunya.

Bukti. Mari kita lihat kontradiksi: misalkan matriks $A$ mempunyai setidaknya dua invers - $B$ dan $C$. Maka menurut definisi, persamaan berikut ini benar:

\[\begin(sejajarkan) & A\cdot B=B\cdot A=E; \\ & A\cdot C=C\cdot A=E. \\ \end(sejajarkan)\]

Dari Lemma 1 kita menyimpulkan bahwa keempat matriks - $A$, $B$, $C$ dan $E$ - adalah kuadrat dengan orde yang sama: $\left[ n\times n \right]$. Oleh karena itu, produk didefinisikan:

Karena perkalian matriks bersifat asosiatif (tetapi tidak komutatif!), kita dapat menulis:

\[\begin(sejajarkan) & B\cdot A\cdot C=\kiri(B\cdot A \kanan)\cdot C=E\cdot C=C; \\ & B\cdot A\cdot C=B\cdot \kiri(A\cdot C \kanan)=B\cdot E=B; \\ & B\cdot A\cdot C=C=B\Panah Kanan B=C. \\ \end(sejajarkan)\]

Kami mendapat satu-satunya pilihan yang mungkin: dua salinan matriks invers adalah sama. Lemmanya terbukti.

Argumen di atas mengulangi hampir kata demi kata bukti keunikan elemen invers untuk semua bilangan real $b\ne 0$. Satu-satunya penambahan yang signifikan adalah dengan mempertimbangkan dimensi matriks.

Namun, kita masih belum mengetahui apakah setiap matriks persegi dapat dibalik. Di sini determinan membantu kita - ini adalah karakteristik utama untuk semua matriks persegi.

Lemma 3. Diberikan matriks $A$. Jika invers matriks $((A)^(-1))$ ada, maka determinan matriks aslinya bukan nol:

\[\kiri| A\kanan|\ne 0\]

Bukti. Kita telah mengetahui bahwa $A$ dan $((A)^(-1))$ adalah matriks persegi dengan ukuran $\left[ n\times n \right]$. Oleh karena itu, untuk masing-masingnya kita dapat menghitung determinannya: $\left| A\kanan|$ dan $\kiri| ((A)^(-1)) \kanan|$. Namun, determinan suatu produk sama dengan produk determinannya:

\[\kiri| A\cdot B \kanan|=\kiri| \kanan|\cdot \kiri| B \kanan|\Panah Kanan \kiri| A\cdot ((A)^(-1)) \kanan|=\kiri| \kanan|\cdot \kiri| ((A)^(-1)) \kanan|\]

Namun menurut definisi, $A\cdot ((A)^(-1))=E$, dan determinan $E$ selalu sama dengan 1, jadi

\[\begin(align) & A\cdot ((A)^(-1))=E; \\ & \kiri| A\cdot ((A)^(-1)) \kanan|=\kiri| Benar|; \\ & \kiri| \kanan|\cdot \kiri| ((A)^(-1)) \kanan|=1. \\ \end(sejajarkan)\]

Hasil kali dua bilangan sama dengan satu hanya jika masing-masing bilangan berikut bukan nol:

\[\kiri| A \kanan|\ne 0;\quad \kiri| ((A)^(-1)) \kanan|\ne 0.\]

Jadi ternyata $\left| \kanan|\ne 0$. Lemmanya terbukti.

Sebenarnya persyaratan ini cukup logis. Sekarang kita akan menganalisis algoritma untuk mencari matriks invers - dan akan menjadi jelas mengapa, dengan determinan nol, pada prinsipnya tidak ada matriks invers.

Namun pertama-tama, mari kita rumuskan definisi “tambahan”:

Definisi. Matriks singular adalah matriks persegi berukuran $\left[ n\times n \right]$ yang determinannya nol.

Dengan demikian, kita dapat menyatakan bahwa setiap matriks yang dapat dibalik adalah non-singular.

Cara mencari invers suatu matriks

Sekarang kita akan mempertimbangkan algoritma universal untuk mencari matriks invers. Secara umum, ada dua algoritma yang diterima secara umum, dan kami juga akan mempertimbangkan algoritma kedua hari ini.

Yang akan dibahas sekarang sangat efektif untuk matriks berukuran $\left[ 2\times 2 \right]$ dan - sebagian - berukuran $\left[ 3\times 3 \right]$. Namun mulai dari ukuran $\left[ 4\times 4 \right]$ lebih baik tidak digunakan. Mengapa - sekarang Anda akan memahami semuanya sendiri.

Penambahan aljabar

Siap-siap. Sekarang akan ada rasa sakit. Tidak, jangan khawatir: perawat cantik dengan rok, stoking renda tidak akan mendatangi Anda dan memberi Anda suntikan di pantat. Semuanya jauh lebih membosankan: penambahan aljabar dan Yang Mulia “Union Matrix” datang kepada Anda.

Mari kita mulai dengan hal utama. Misalkan ada matriks persegi berukuran $A=\left[ n\times n \right]$, yang elemen-elemennya disebut $((a)_(ij))$. Kemudian untuk setiap elemen tersebut kita dapat mendefinisikan komplemen aljabar:

Definisi. Komplemen aljabar $((A)_(ij))$ pada elemen $((a)_(ij))$ yang terletak pada baris ke-$i$ dan kolom ke-$j$ pada matriks $A=\left[ n \times n \right]$ adalah konstruksi formulir

\[((A)_(ij))=((\kiri(-1 \kanan))^(i+j))\cdot M_(ij)^(*)\]

Dimana $M_(ij)^(*)$ adalah determinan matriks yang diperoleh dari $A$ asli dengan menghapus baris ke-$i$ dan kolom ke-$j$ yang sama.

Lagi. Komplemen aljabar elemen matriks dengan koordinat $\left(i;j \right)$ dinotasikan sebagai $((A)_(ij))$ dan dihitung berdasarkan skema:

Pertama, kita menghapus kolom $i$-baris dan $j$-th dari matriks asli. Kita memperoleh matriks persegi baru, dan kita menyatakan determinannya sebagai $M_(ij)^(*)$.
Kemudian kita mengalikan determinan ini dengan $((\left(-1 \right))^(i+j))$ - pada awalnya ekspresi ini mungkin tampak mengejutkan, tetapi pada dasarnya kita hanya mencari tahu tanda di depan $M_(ij)^(*) $.
Kami menghitung dan mendapatkan nomor tertentu. Itu. penjumlahan aljabar justru berupa bilangan, dan bukan matriks baru, dll.

Matriks $M_(ij)^(*)$ sendiri disebut minor tambahan pada elemen $((a)_(ij))$. Dan dalam pengertian ini, definisi komplemen aljabar di atas adalah kasus khusus dari definisi yang lebih kompleks - apa yang kita bahas dalam pelajaran tentang determinan.

Catatan penting. Sebenarnya, dalam matematika “dewasa”, penjumlahan aljabar didefinisikan sebagai berikut:

Kami mengambil $k$ baris dan $k$ kolom dalam matriks persegi. Di perpotongannya kita mendapatkan matriks berukuran $\left[ k\times k \right]$ - determinannya disebut minor berorde $k$ dan dilambangkan dengan $((M)_(k))$.

Kemudian kita mencoret baris $k$ dan kolom $k$ yang “dipilih” ini. Sekali lagi Anda mendapatkan matriks persegi - determinannya disebut minor tambahan dan dilambangkan dengan $M_(k)^(*)$.

Kalikan $M_(k)^(*)$ dengan $((\left(-1 \right))^(t))$, dimana $t$ adalah (perhatian sekarang!) jumlah semua baris yang dipilih dan kolom. Ini akan menjadi penjumlahan aljabar.

Lihatlah langkah ketiga: sebenarnya ada jumlah istilah $2k$! Hal lainnya adalah untuk $k=1$ kita hanya akan mendapatkan 2 suku - ini akan menjadi $i+j$ yang sama - "koordinat" dari elemen $((a)_(ij))$ tempat kita berada mencari komplemen aljabar.

Jadi hari ini kami menggunakan definisi yang sedikit disederhanakan. Tapi seperti yang akan kita lihat nanti, itu sudah lebih dari cukup. Hal berikut ini jauh lebih penting:

Definisi. Matriks gabungan $S$ dengan matriks persegi $A=\left[ n\times n \right]$ adalah matriks baru berukuran $\left[ n\times n \right]$, yang diperoleh dari $A$ dengan mengganti $(( a)_(ij))$ dengan penjumlahan aljabar $((A)_(ij))$:

\\Panah Kanan S=\kiri[ \begin(matriks) ((A)_(11)) & ((A)_(12)) & ... & ((A)_(1n)) \\ (( A)_(21)) & ((A)_(22)) & ... & ((A)_(2n)) \\ ... & ... & ... & ... \\ ((A)_(n1)) & ((A)_(n2)) & ... & ((A)_(nn)) \\\end(matriks) \kanan]\]

Pikiran pertama yang muncul pada saat realisasi definisi ini adalah “berapa banyak yang harus dihitung!” Tenang: Anda harus menghitung, tapi jangan terlalu banyak. :)

Ya, semua ini sangat bagus, tapi mengapa itu perlu? Tapi kenapa.

Teorema utama

Mari kita kembali sedikit. Ingat, Lemma 3 menyatakan bahwa matriks yang dapat dibalik $A$ selalu non-singular (yaitu determinannya bukan nol: $\left| A \right|\ne 0$).

Jadi, yang terjadi juga sebaliknya: jika matriks $A$ tidak tunggal, maka matriks tersebut selalu dapat dibalik. Dan bahkan ada skema pencarian untuk $((A)^(-1))$. Coba lihat:

Teorema matriks terbalik. Misalkan matriks persegi $A=\left[ n\times n \right]$ diberikan, dan determinannya bukan nol: $\left| \kanan|\ne 0$. Maka invers matriks $((A)^(-1))$ ada dan dihitung dengan rumus:

\[((A)^(-1))=\frac(1)(\kiri| A \kanan|)\cdot ((S)^(T))\]

Dan sekarang - semuanya sama, tetapi dengan tulisan tangan yang dapat dibaca. Untuk mencari matriks invers, Anda memerlukan:

Hitung determinan $\left| A \right|$ dan pastikan bukan nol.
Bangun matriks gabungan $S$, mis. hitung 100.500 penjumlahan aljabar $((A)_(ij))$ dan letakkan di tempat $((a)_(ij))$.
Ubah urutan matriks $S$, lalu kalikan dengan bilangan $q=(1)/(\left| A \right|)\;$.

Itu saja! Matriks invers $((A)^(-1))$ telah ditemukan. Mari kita lihat contohnya:

\[\kiri[ \begin(matriks) 3 & 1 \\ 5 & 2 \\\end(matriks) \kanan]\]

Larutan. Mari kita periksa reversibilitasnya. Mari kita hitung determinannya:

\[\kiri| A\kanan|=\kiri| \begin(matriks) 3 & 1 \\ 5 & 2 \\\end(matriks) \kanan|=3\cdot 2-1\cdot 5=6-5=1\]

Penentunya berbeda dari nol. Artinya matriks tersebut dapat dibalik. Mari kita buat matriks gabungan:

Mari kita hitung penjumlahan aljabarnya:

\[\begin(sejajarkan) & ((A)_(11))=((\kiri(-1 \kanan))^(1+1))\cdot \kiri| 2 \kanan|=2; \\ & ((A)_(12))=((\kiri(-1 \kanan))^(1+2))\cdot \kiri| 5 \kanan|=-5; \\ & ((A)_(21))=((\kiri(-1 \kanan))^(2+1))\cdot \kiri| 1 \kanan|=-1; \\ & ((A)_(22))=((\kiri(-1 \kanan))^(2+2))\cdot \kiri| 3\kanan|=3. \\ \end(sejajarkan)\]

Perlu diperhatikan: determinan |2|, |5|, |1| dan |3| adalah determinan matriks berukuran $\left[ 1\times 1 \right]$, dan bukan modul. Itu. Jika ada angka negatif pada determinannya, maka “minus” tidak perlu dihilangkan.

Secara total, matriks gabungan kita terlihat seperti ini:

\[((A)^(-1))=\frac(1)(\kiri| A \kanan|)\cdot ((S)^(T))=\frac(1)(1)\cdot ( (\kiri[ \begin(array)(*(35)(r)) 2 & -5 \\ -1 & 3 \\\end(array) \kanan])^(T))=\kiri[ \begin (array)(*(35)(r)) 2 & -1 \\ -5 & 3 \\\end(array) \kanan]\]

Oke, semuanya sudah berakhir. Sekarang. Masalah terpecahkan.

Menjawab. $\kiri[ \begin(array)(*(35)(r)) 2 & -1 \\ -5 & 3 \\\end(array) \kanan]$

Tugas. Temukan matriks invers:

\[\kiri[ \begin(array)(*(35)(r)) 1 & -1 & 2 \\ 0 & 2 & -1 \\ 1 & 0 & 1 \\\end(array) \kanan] \]

Larutan. Kami menghitung determinannya lagi:

\[\mulai(sejajarkan) & \kiri| \begin(array)(*(35)(r)) 1 & -1 & 2 \\ 0 & 2 & -1 \\ 1 & 0 & 1 \\\end(array) \kanan|=\begin(matriks ) \kiri(1\cdot 2\cdot 1+\kiri(-1 \kanan)\cdot \kiri(-1 \kanan)\cdot 1+2\cdot 0\cdot 0 \kanan)- \\ -\kiri (2\cdot 2\cdot 1+\kiri(-1 \kanan)\cdot 0\cdot 1+1\cdot \kiri(-1 \kanan)\cdot 0 \kanan) \\\end(matriks)= \ \ & =\kiri(2+1+0 \kanan)-\kiri(4+0+0 \kanan)=-1\ne 0. \\ \end(sejajarkan)\]

Penentunya bukan nol—matriksnya dapat dibalik. Tapi sekarang ini akan menjadi sangat sulit: kita perlu menghitung sebanyak 9 (sembilan, bajingan!) penjumlahan aljabar. Dan masing-masingnya akan berisi determinan $\left[ 2\times 2 \right]$. Terbang:

\[\begin(matriks) ((A)_(11))=((\kiri(-1 \kanan))^(1+1))\cdot \kiri| \begin(matriks) 2 & -1 \\ 0 & 1 \\\end(matriks) \kanan|=2; \\ ((A)_(12))=((\kiri(-1 \kanan))^(1+2))\cdot \kiri| \begin(matriks) 0 & -1 \\ 1 & 1 \\\end(matriks) \kanan|=-1; \\ ((A)_(13))=((\kiri(-1 \kanan))^(1+3))\cdot \kiri| \begin(matriks) 0 & 2 \\ 1 & 0 \\\end(matriks) \kanan|=-2; \\ ... \\ ((A)_(33))=((\kiri(-1 \kanan))^(3+3))\cdot \kiri| \begin(matriks) 1 & -1 \\ 0 & 2 \\\end(matriks) \kanan|=2; \\ \end(matriks)\]

Singkatnya, matriks gabungan akan terlihat seperti ini:

Oleh karena itu, matriks inversnya adalah:

\[((A)^(-1))=\frac(1)(-1)\cdot \kiri[ \begin(matriks) 2 & -1 & -2 \\ 1 & -1 & -1 \\ -3 & 1 & 2 \\\end(matriks) \kanan]=\kiri[ \begin(array)(*(35)(r))-2 & -1 & 3 \\ 1 & 1 & -1 \ \2 & 1 & -2 \\\end(array) \kanan]\]

Itu dia. Inilah jawabannya.

Menjawab. $\kiri[ \begin(array)(*(35)(r)) -2 & -1 & 3 \\ 1 & 1 & -1 \\ 2 & 1 & -2 \\\end(array) \kanan ]$

Seperti yang Anda lihat, di akhir setiap contoh kami melakukan pemeriksaan. Dalam hal ini, catatan penting:

Jangan malas untuk memeriksanya. Kalikan matriks asli dengan matriks invers yang ditemukan - Anda akan mendapatkan $E$.

Melakukan pemeriksaan ini jauh lebih mudah dan cepat daripada mencari kesalahan dalam perhitungan selanjutnya ketika, misalnya, Anda menyelesaikan persamaan matriks.

Cara alternatif

Seperti yang saya katakan, teorema matriks invers berfungsi baik untuk ukuran $\left[ 2\times 2 \right]$ dan $\left[ 3\times 3 \right]$ (dalam kasus terakhir, ini tidak terlalu "hebat" " ), tetapi untuk matriks yang lebih besar, kesedihan dimulai.

Namun jangan khawatir: ada algoritme alternatif yang dapat digunakan untuk mencari invers dengan tenang bahkan untuk matriks $\left[ 10\times 10 \right]$. Namun, seperti yang sering terjadi, untuk mempertimbangkan algoritma ini kita memerlukan sedikit latar belakang teoritis.

Transformasi dasar

Di antara semua kemungkinan transformasi matriks, ada beberapa transformasi khusus - yang disebut transformasi dasar. Tepatnya ada tiga transformasi seperti itu:

Perkalian. Anda dapat mengambil baris (kolom) $i$th dan mengalikannya dengan angka berapa saja $k\ne 0$;
Tambahan. Tambahkan ke baris (kolom) ke-$i$ ke-$j$ lainnya (kolom) dikalikan dengan angka berapa pun $k\ne 0$ (tentu saja Anda dapat melakukan $k=0$, tapi berapa hasilnya? titik? ? Tidak ada yang akan berubah).
Penyusunan kembali. Ambil baris (kolom) $i$th dan $j$th dan tukar tempat.

Mengapa transformasi ini disebut transformasi dasar (untuk matriks besar, transformasi ini tidak terlihat begitu mendasar) dan mengapa hanya ada tiga transformasi - pertanyaan-pertanyaan ini berada di luar cakupan pelajaran hari ini. Oleh karena itu, kami tidak akan membahas secara detail.

Hal lain yang penting: kita harus melakukan semua penyimpangan ini pada matriks adjoint. Ya, ya: Anda tidak salah dengar. Sekarang akan ada definisi lain - yang terakhir dalam pelajaran hari ini.

Matriks adjoin

Pastinya di sekolah kamu menyelesaikan sistem persamaan dengan menggunakan metode penjumlahan. Nah, kurangi yang lain dari satu baris, kalikan beberapa baris dengan angka - itu saja.

Jadi: sekarang semuanya akan sama, tetapi dengan cara yang “dewasa”. Siap?

Definisi. Misalkan diberikan matriks $A=\left[ n\times n \right]$ dan matriks identitas $E$ dengan ukuran yang sama $n$. Kemudian matriks adjoin $\left[ A\left| Benar. \kanan]$ adalah matriks baru berukuran $\left[ n\times 2n \right]$ yang terlihat seperti ini:

\[\kiri[ A\kiri| Benar. \kanan]=\kiri[ \begin(array)(rrrr|rrrr)((a)_(11)) & ((a)_(12)) & ... & ((a)_(1n)) & 1 & 0 & ... & 0 \\((a)_(21)) & ((a)_(22)) & ... & ((a)_(2n)) & 0 & 1 & ... & 0 \\... & ... & ... & ... & ... & ... & ... & ... \\((a)_(n1)) & ((a)_(n2)) & ... & ((a)_(nn)) & 0 & 0 & ... & 1 \\\end(array) \kanan]\]

Singkatnya, kita ambil matriks $A$, di sebelah kanan kita tetapkan matriks identitas $E$ dengan ukuran yang diperlukan, kita pisahkan dengan garis vertikal untuk keindahan - ini dia adjointnya. :)

Apa menariknya? Inilah yang:

Dalil. Biarkan matriks $A$ dapat dibalik. Perhatikan matriks adjoin $\left[ A\left| Benar. \kanan]$. Jika menggunakan konversi string dasar bawa ke bentuk $\left[ E\left| Terang. \kanan]$, yaitu dengan mengalikan, mengurangi dan menyusun ulang baris-baris sehingga diperoleh dari $A$ matriks $E$ di sebelah kanan, maka matriks $B$ yang diperoleh di sebelah kiri adalah invers dari $A$:

\[\kiri[ A\kiri| Benar. \kanan]\ke \kiri[ E\kiri| Terang. \kanan]\Panah Kanan B=((A)^(-1))\]

Sesederhana itu! Singkatnya, algoritma untuk mencari matriks invers terlihat seperti ini:

Tulis matriks adjoin $\left[ A\left| Benar. \kanan]$;
Lakukan konversi string dasar hingga $E$ muncul, bukan $A$;
Tentu saja, sesuatu juga akan muncul di sebelah kiri - matriks $B$ tertentu. Hal ini justru sebaliknya;
LABA!:)

Tentu saja, hal ini lebih mudah diucapkan daripada dilakukan. Jadi mari kita lihat beberapa contoh: untuk ukuran $\left[ 3\times 3 \right]$ dan $\left[ 4\times 4 \right]$.

Tugas. Temukan matriks invers:

\[\kiri[ \begin(array)(*(35)(r)) 1 & 5 & 1 \\ 3 & 2 & 1 \\ 6 & -2 & 1 \\\end(array) \kanan]\ ]

Larutan. Kami membuat matriks adjoin:

\[\kiri[ \begin(array)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 3 & 2 & 1 & 0 & 1 & 0 \\ 6 & -2 & 1 & 0 & 0 & 1 \\\end(array) \kanan]\]

Karena kolom terakhir matriks asli diisi dengan satu, kurangi baris pertama dari sisanya:

\[\begin(align) & \left[ \begin(array)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 3 & 2 & 1 & 0 & 1 & 0 \\ 6 & - 2 & 1 & 0 & 0 & 1 \\\end(array) \kanan]\begin(matriks) \panah bawah \\ -1 \\ -1 \\\end(matriks)\ke \\ & \ke \kiri [ \begin(array)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 5 & -7 & 0 & -1 & 0 & 1 \\\end(array) \kanan] \\ \end(sejajarkan)\]

Tidak ada unit lagi, kecuali baris pertama. Tapi kami tidak menyentuhnya, jika tidak, unit yang baru dihapus akan mulai “berkembang biak” di kolom ketiga.

Tapi kita bisa mengurangi baris kedua dua kali dari baris terakhir - kita mendapatkan satu di sudut kiri bawah:

\[\begin(align) & \left[ \begin(array)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 5 & -7 & 0 & -1 & 0 & 1 \\\end(array) \kanan]\begin(matriks) \ \\ \panah bawah \\ -2 \\\end(matriks)\ke \\ & \kiri [ \begin(array)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\end(array) \kanan] \\ \end(sejajarkan)\]

Sekarang kita dapat mengurangi baris terakhir dari baris pertama dan dua kali dari baris kedua - dengan cara ini kita “menghilangkan” kolom pertama:

\[\begin(align) & \left[ \begin(array)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\end(array) \kanan]\begin(matriks) -1 \\ -2 \\ \uparrow \\\end(matriks)\ke \\ & \ ke \kiri[ \begin(array)(rrr|rrr) 0 & 6 & 1 & 0 & 2 & -1 \\ 0 & -1 & 0 & -3 & 5 & -2 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\end(array) \kanan] \\ \end(sejajarkan)\]

Kalikan baris kedua dengan −1, lalu kurangi baris pertama sebanyak 6 kali dan tambahkan baris terakhir sebanyak 1 kali:

\[\begin(align) & \left[ \begin(array)(rrr|rrr) 0 & 6 & 1 & 0 & 2 & -1 \\ 0 & -1 & 0 & -3 & 5 & -2 \ \ 1 & -1 & 0 & 1 & -2 & 1 \\\end(array) \kanan]\begin(matriks) \ \\ \kiri| \cdot \kiri(-1 \kanan) \kanan. \\ \ \\\end(matriks)\ke \\ & \ke \kiri[ \begin(array)(rrr|rrr) 0 & 6 & 1 & 0 & 2 & -1 \\ 0 & 1 & 0 & 3 & -5 & 2 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\end(array) \kanan]\begin(matriks) -6 \\ \updownarrow \\ +1 \\\end (matriks)\ke \\ & \ke \kiri[ \begin(array)(rrr|rrr) 0 & 0 & 1 & -18 & 32 & -13 \\ 0 & 1 & 0 & 3 & -5 & 2 \\ 1 & 0 & 0 & 4 & -7 & 3 \\\end(array) \kanan] \\ \end(align)\]

Yang tersisa hanyalah menukar jalur 1 dan 3:

\[\kiri[ \begin(array)(rrr|rrr) 1 & 0 & 0 & 4 & -7 & 3 \\ 0 & 1 & 0 & 3 & -5 & 2 \\ 0 & 0 & 1 & - 18 & 32 & -13 \\\end(array) \kanan]\]

Siap! Di sebelah kanan adalah matriks invers yang diperlukan.

Menjawab. $\kiri[ \begin(array)(*(35)(r))4 & -7 & 3 \\ 3 & -5 & 2 \\ -18 & 32 & -13 \\\end(array) \kanan ]$

Tugas. Temukan matriks invers:

\[\kiri[ \begin(matriks) 1 & 4 & 2 & 3 \\ 1 & -2 & 1 & -2 \\ 1 & -1 & 1 & 1 \\ 0 & -10 & -2 & -5 \\\end(matriks) \kanan]\]

Larutan. Kami membuat tambahan lagi:

\[\kiri[ \begin(array)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 1 & -2 & 1 & -2 & 0 & 1 & 0 & 0 \ \ 1 & -1 & 1 & 1 & 0 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\\end(array) \kanan]\]

Mari kita menangis sedikit, bersedih karena banyaknya yang harus kita hitung sekarang... dan mulailah menghitung. Pertama, mari kita “menghilangkan” kolom pertama dengan mengurangi baris 1 dari baris 2 dan 3:

\[\begin(align) & \left[ \begin(array)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 1 & -2 & 1 & -2 & 0 & 1 & 0 & 0 \\ 1 & -1 & 1 & 1 & 0 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\\end(array) \kanan]\begin(matriks) \panah bawah \\ -1 \\ -1 \\ \ \\\end(matriks)\ke \\ & \ke \kiri[ \begin(array)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 0 & -6 & -1 & -5 & -1 & 1 & 0 & 0 \\ 0 & -5 & -1 & -2 & -1 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\\end(array) \kanan] \\ \end(sejajarkan)\]

Kami melihat terlalu banyak “kontra” di baris 2-4. Kalikan ketiga baris dengan −1, lalu habiskan kolom ketiga dengan mengurangi baris 3 dari sisanya:

\[\begin(align) & \left[ \begin(array)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 0 & -6 & -1 & -5 & - 1 & 1 & 0 & 0 \\ 0 & -5 & -1 & -2 & -1 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\ \end(array) \kanan]\begin(matriks) \ \\ \kiri| \cdot \kiri(-1 \kanan) \kanan. \\ \kiri| \cdot \kiri(-1 \kanan) \kanan. \\ \kiri| \cdot \kiri(-1 \kanan) \kanan. \\\end(matriks)\ke \\ & \ke \kiri[ \begin(array)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 0 & 6 & 1 & 5 & 1 & -1 & 0 & 0 \\ 0 & 5 & 1 & 2 & 1 & 0 & -1 & 0 \\ 0 & 10 & 2 & 5 & 0 & 0 & 0 & -1 \\ \end (array) \kanan]\begin(matriks) -2 \\ -1 \\ \updownarrow \\ -2 \\\end(matriks)\to \\ & \to \left[ \begin(array)( rrrr| rrrr) 1 & -6 & 0 & -1 & -1 & 0 & 2 & 0 \\ 0 & 1 & 0 & 3 & 0 & -1 & 1 & 0 \\ 0 & 5 & 1 & 2 & 1 & 0 & -1 & 0 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end(array) \kanan] \\ \end(sejajarkan)\]

Sekarang adalah waktunya untuk “menggoreng” kolom terakhir dari matriks asli: kurangi baris 4 dari sisanya:

\[\begin(align) & \left[ \begin(array)(rrrr|rrrr) 1 & -6 & 0 & -1 & -1 & 0 & 2 & 0 \\ 0 & 1 & 0 & 3 & 0 & -1 & 1 & 0 \\ 0 & 5 & 1 & 2 & 1 & 0 & -1 & 0 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end(array ) \kanan]\begin(matriks) +1 \\ -3 \\ -2 \\ \uparrow \\\end(matriks)\ke \\ & \ke \kiri[ \begin(array)(rrrr|rrrr) 1 & -6 & 0 & 0 & -3 & 0 & 4 & -1 \\ 0 & 1 & 0 & 0 & 6 & -1 & -5 & 3 \\ 0 & 5 & 1 & 0 & 5 & 0 & -5 & 2 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end(array) \kanan] \\ \end(sejajarkan)\]

Lemparan terakhir: “bakar habis” kolom kedua dengan mengurangi baris 2 dari baris 1 dan 3:

\[\begin(align) & \left[ \begin(array)(rrrr|rrrr) 1 & -6 & 0 & 0 & -3 & 0 & 4 & -1 \\ 0 & 1 & 0 & 0 & 6 & -1 & -5 & 3 \\ 0 & 5 & 1 & 0 & 5 & 0 & -5 & 2 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end( array) \kanan]\begin(matriks) 6 \\ \updownarrow \\ -5 \\ \ \\\end(matrix)\to \\ & \to \left[ \begin(array)(rrrr|rrrr) 1 & 0 & 0 & 0 & 33 & -6 & -26 & -17 \\ 0 & 1 & 0 & 0 & 6 & -1 & -5 & 3 \\ 0 & 0 & 1 & 0 & -25 & 5 & 20 & -13 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end(array) \kanan] \\ \end(sejajarkan)\]

Dan lagi matriks identitasnya ada di sebelah kiri, artinya inversnya ada di sebelah kanan. :)

Menjawab. $\kiri[ \begin(matriks) 33 & -6 & -26 & 17 \\ 6 & -1 & -5 & 3 \\ -25 & 5 & 20 & -13 \\ -2 & 0 & 2 & - 1 \\\end(matriks) \kanan]$

Oke, semuanya sudah berakhir. Sekarang. Lakukan pengecekan sendiri - saya kacau. :)

Mirip dengan kebalikan di banyak properti.

YouTube ensiklopedis

1 / 5

✪ Matriks terbalik (2 cara mencari)

✪ Cara mencari invers suatu matriks - bezbotvy

✪ Matriks terbalik #1

✪ Menyelesaikan sistem persamaan menggunakan metode matriks terbalik - bezbotvy

✪ Matriks Terbalik

Subtitle

Sifat-sifat matriks invers

det A − 1 = 1 det A (\displaystyle \det A^(-1)=(\frac (1)(\det A))), Di mana det (\displaystyle \\det ) menunjukkan determinan.
(A B) − 1 = B − 1 A − 1 (\displaystyle \ (AB)^(-1)=B^(-1)A^(-1)) untuk dua matriks persegi yang dapat dibalik A (\gaya tampilan A) Dan B (\gaya tampilan B).
(AT) − 1 = (A − 1) T (\displaystyle \ (A^(T))^(-1)=(A^(-1))^(T)), Di mana (. . .) T (\displaystyle (...)^(T)) menunjukkan matriks yang ditransposisikan.
(k A) − 1 = k − 1 A − 1 (\displaystyle \ (kA)^(-1)=k^(-1)A^(-1)) untuk koefisien apa pun k ≠ 0 (\displaystyle k\tidak =0).
E − 1 = E (\displaystyle \E^(-1)=E).
Jika perlu menyelesaikan sistem persamaan linier, (b adalah vektor bukan nol) di mana x (\gaya tampilan x) adalah vektor yang diinginkan, dan jika A − 1 (\gaya tampilan A^(-1)) ada, kalau begitu x = A − 1 b (\displaystyle x=A^(-1)b). Jika tidak, maka dimensi ruang solusi lebih besar dari nol, atau tidak ada solusi sama sekali.

Metode untuk mencari matriks invers

Jika matriksnya dapat dibalik, maka untuk mencari matriks inversnya dapat menggunakan salah satu cara berikut:

Metode eksak (langsung).

Metode Gauss-Jordan

Mari kita ambil dua matriks: the A dan lajang E. Mari kita sajikan matriksnya A ke matriks identitas menggunakan metode Gauss-Jordan, menerapkan transformasi sepanjang baris (Anda juga dapat menerapkan transformasi sepanjang kolom, tetapi tidak dicampur). Setelah menerapkan setiap operasi pada matriks pertama, terapkan operasi yang sama pada matriks kedua. Ketika reduksi matriks pertama menjadi bentuk satuan selesai, matriks kedua akan sama dengan SEBUAH−1.

Bila menggunakan metode Gaussian, matriks pertama akan dikalikan di sebelah kiri dengan salah satu matriks elementer Λ i (\displaystyle \Lambda _(i))(matriks transveksi atau diagonal dengan satuan pada diagonal utama, kecuali satu posisi):

Λ 1 ⋅ ⋯ ⋅ Λ n ⋅ A = Λ A = E ⇒ Λ = A − 1 (\displaystyle \Lambda _(1)\cdot \dots \cdot \Lambda _(n)\cdot A=\Lambda A=E \Panah Kanan \Lambda =A^(-1)). Λ m = [ 1 … 0 − a 1 m / am m 0 … 0 … 0 … 1 − am − 1 m / am + 1 m / am m 1 … 0 … 0 … 0 − an m / a m m 0 … 1 ] (\displaystyle \Lambda _(m)=(\begin(bmatrix)1&\dots &0&-a_(1m)/a_(mm)&0&\dots &0\\ &&&\titik &&&\\0&\titik &1&-a_(m-1m)/a_(mm)&0&\titik &0\\0&\titik &0&1/a_(mm)&0&\titik &0\\0&\titik &0&-a_( m+1m)/a_(mm)&1&\titik &0\\&&&\titik &&&\\0&\titik &0&-a_(nm)/a_(mm)&0&\titik &1\end(bmatrix))).

Matriks kedua setelah menerapkan semua operasi akan sama dengan Λ (\displaystyle \Lambda), yaitu, itu akan menjadi yang diinginkan. Kompleksitas algoritma - O (n 3) (\displaystyle O(n^(3))).

Menggunakan matriks komplemen aljabar

Matriks kebalikan dari matriks A (\gaya tampilan A), dapat direpresentasikan dalam bentuk

A − 1 = adj (A) det (A) (\displaystyle (A)^(-1)=(((\mbox(adj))(A)) \over (\det(A))))

Di mana adj (A) (\displaystyle (\mbox(adj))(A))- matriks adjoin;

Kompleksitas algoritma bergantung pada kompleksitas algoritma untuk menghitung determinan O det dan sama dengan O(n²)·O det.

Menggunakan Dekomposisi LU/LUP

Persamaan matriks A X = Saya n (\displaystyle AX=I_(n)) untuk matriks invers X (\gaya tampilan X) dapat dianggap sebagai koleksi n (\gaya tampilan n) sistem formulir A x = b (\displaystyle Kapak=b). Mari kita tunjukkan saya (\gaya tampilan i) kolom matriks X (\gaya tampilan X) melalui X saya (\gaya tampilan X_(i)); Kemudian A X i = e i (\displaystyle AX_(i)=e_(i)), i = 1 , … , n (\displaystyle i=1,\ltitik ,n),karena saya (\gaya tampilan i) kolom matriks Saya n (\displaystyle I_(n)) adalah vektor satuan e i (\displaystyle e_(i)). dengan kata lain, mencari matriks invers berarti menyelesaikan n persamaan dengan matriks yang sama dan ruas kanan yang berbeda. Setelah melakukan dekomposisi LUP (waktu O(n³), menyelesaikan masing-masing n persamaan membutuhkan waktu O(n²), sehingga bagian pekerjaan ini juga memerlukan waktu O(n³).

Jika matriks A nonsingular, maka dekomposisi LUP dapat dihitung PA = LU (\displaystyle PA=LU). Membiarkan PA = B (\gaya tampilan PA=B), B − 1 = D (\displaystyle B^(-1)=D). Kemudian dari sifat-sifat matriks invers kita dapat menulis: D = U − 1 L − 1 (\displaystyle D=U^(-1)L^(-1)). Jika Anda mengalikan persamaan ini dengan U dan L, Anda akan mendapatkan dua persamaan bentuk UD = L − 1 (\displaystyle UD=L^(-1)) Dan D L = U − 1 (\displaystyle DL=U^(-1)). Persamaan pertama adalah sistem persamaan linier n² untuk n (n + 1) 2 (\displaystyle (\frac (n(n+1))(2))) yang sisi kanannya diketahui (dari sifat-sifat matriks segitiga). Yang kedua juga mewakili sistem persamaan linear n² untuk n (n − 1) 2 (\displaystyle (\frac (n(n-1))(2))) yang diketahui sisi kanannya (juga dari sifat-sifat matriks segitiga). Bersama-sama mereka mewakili sistem persamaan n². Dengan menggunakan persamaan tersebut, kita dapat menentukan secara rekursif seluruh n² elemen matriks D. Kemudian dari persamaan (PA) −1 = A −1 P −1 = B −1 = D. kita memperoleh persamaan tersebut A − 1 = DP (\displaystyle A^(-1)=DP).

Dalam hal menggunakan dekomposisi LU, tidak diperlukan permutasi kolom-kolom matriks D, tetapi solusinya mungkin berbeda meskipun matriks A berbentuk nonsingular.

Kompleksitas algoritmanya adalah O(n³).

Metode berulang

metode Schultz

( Ψ k = E − A U k , U k + 1 = U k ∑ i = 0 n Ψ k i (\displaystyle (\begin(cases)\Psi _(k)=E-AU_(k),\\U_( k+1)=U_(k)\jumlah _(i=0)^(n)\Psi _(k)^(i)\end(kasus)))

Perkiraan kesalahan

Memilih Pendekatan Awal

Masalah pemilihan perkiraan awal dalam proses inversi matriks berulang yang dipertimbangkan di sini tidak memungkinkan kita untuk memperlakukannya sebagai metode universal independen yang bersaing dengan metode inversi langsung, misalnya, berdasarkan dekomposisi matriks LU. Ada beberapa rekomendasi untuk memilih kamu 0 (\gaya tampilan U_(0)), memastikan terpenuhinya kondisi ρ (Ψ 0) < 1 {\displaystyle \rho (\Psi _{0})<1} (jari-jari spektral matriks kurang dari satu), yang diperlukan dan cukup untuk konvergensi proses. Namun dalam hal ini, pertama-tama perlu diketahui dari atas estimasi spektrum matriks A atau matriks yang dapat dibalik. AT (\displaystyle AA^(T))(yaitu, jika A adalah matriks definit positif simetris dan ρ (A) ≤ β (\displaystyle \rho (A)\leq \beta ), lalu kamu bisa mengambilnya kamu 0 = α E (\displaystyle U_(0)=(\alpha )E), Di mana ; jika A adalah matriks non-tunggal sembarang dan ρ (A A T) ≤ β (\displaystyle \rho (AA^(T))\leq \beta ), lalu mereka percaya U 0 = α A T (\displaystyle U_(0)=(\alpha )A^(T)), dimana juga α ∈ (0 , 2 β) (\displaystyle \alpha \di \kiri(0,(\frac (2)(\beta ))\kanan)); Anda tentu saja dapat menyederhanakan situasi dan memanfaatkan fakta tersebut ρ (A A T) ≤ k A A T k (\displaystyle \rho (AA^(T))\leq (\mathcal (k))AA^(T)(\mathcal (k))), meletakkan U 0 = A T ‖ A A T ‖ (\displaystyle U_(0)=(\frac (A^(T))(\|AA^(T)\|)))). Kedua, ketika menentukan matriks awal dengan cara ini, tidak ada jaminan bahwa ‖ Ψ 0 ‖ (\displaystyle \|\Psi _(0)\|) akan menjadi kecil (bahkan mungkin akan menjadi kecil ‖ Ψ 0 ‖ > 1 (\displaystyle \|\Psi _(0)\|>1)), dan tingkat konvergensi tingkat tinggi tidak akan segera terungkap.

Contoh

Matriks 2x2

Tidak dapat menguraikan ekspresi (kesalahan sintaksis): (\displaystyle \mathbf(A)^(-1) = \begin(bmatrix) a & b \\ c & d \\ \end(bmatrix)^(-1) = \ frac (1)(\det(\mathbf(A))) \begin& \!\!-b \\ -c & \,a \\ \end(bmatrix) = \frac(1)(ad - bc) \ mulai (bmatrix) \,\,\,d & \!\!-b\\ -c & \,a \\ \end(bmatrix).)

Inversi matriks 2x2 hanya dimungkinkan jika a d − b c = det A ≠ 0 (\displaystyle ad-bc=\det A\neq 0).

Untuk menyelesaikan sistem persamaan linear (3) terhadap x 1 Mari kita gunakan metode Gaussian.

Sistem persamaan linear (2) lainnya diselesaikan dengan cara yang sama.

Akhirnya sekelompok vektor kolom x 1 , x 2 , ..., xn membentuk matriks invers A-1.

Perhatikan bahwa setelah menemukan matriks permutasi P 1 , P 2 , ... , P n-1 dan matriks pengecualian M 1, M 2, ..., M n-1(lihat halaman Metode eliminasi Gaussian) dan membuat matriks

M=M n-1 P n-1 ...M 2 P 2 M 1 P 1 ,

sistem (2) dapat ditransformasikan ke dalam bentuk

MAx 1 = Saya 1,
MAx 2 = Saya 2,
......
MAx n = Saya n .

Dari sini adalah x 1 ,x 2 , ..., xn, dengan sisi kanan yang berbeda Saya 1, Saya 2, ..., Saya n.

Saat menghitung matriks invers, akan lebih mudah untuk menambahkan matriks identitas ke sisi kanan matriks asli dan menerapkan metode Gaussian dalam arah maju dan mundur.

Mari kita lihat ini dengan sebuah contoh.